题目内容
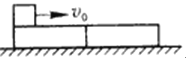
【题目】如图所示，在光滑地面上并排放两个相同的木块，长度皆为ｌ＝1.00ｍ，在左边木块的最左端放一小金属块，它的质量等于一个木块的质量，开始小金属块以初速度ｖ0＝2.00ｍ／ｓ向右滑动，金属块与木块之间的滑动摩擦因数μ＝0.10，ｇ取10ｍ／ｓ2，求：木块的最后速度．
【答案】ｖ1＝1／3ｍ／ｓ，ｖ2＝5／6ｍ／ｓ
【解析】假设金属块没有离开第一块长木板，移动的相对距离为ｘ，由动量守恒定律，得ｍｖ0＝3ｍｖ，
ｍｖ02＝
3ｍｖ2＋μｍｇｘ，
解得ｘ＝4ｍ／3＞Ｌ，不合理，∴金属块一定冲上第二块木板．
以整个系统为研究对象，由动量定律及能量关系，当金属块在第一块木板上时
ｍｖ0＝ｍｖ0′＋2ｍｖ1，
ｍｖ02＝
ｍｖ0′2＋
·2ｍｖ12＋μｍｇｌ．
ｍｖ0＝ｍｖ1＋2ｍｖ2
ｍｖ02＝
ｍｖ12＋
2ｍ·ｖ22＋μｍｇ（ｌ＋ｘ）．
联立解得：ｖ1＝
ｍ／ｓ，ｖ2＝
ｍ／ｓ，ｘ＝0.25ｍ．
练习册系列答案
相关题目
