题目内容
9．
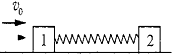光滑水平面上静置两个小木块1和2，其质量分别为m1=1.0kg、m2=4.0kg，它们中间用一根轻质弹簧相连．一颗水平飞行的子弹质量为m=50.0g，以v0=500m/s的速度在极短时间内射穿两木块，已知射穿木块1后子弹的速度变为原来的$\frac{3}{5}$，且子弹损失的动能为射穿木块2损失动能的2倍．求系统运动过程中弹簧的最大弹性势能．
分析 子弹穿过1时，由于时间极短，弹簧与2没有参与相互作用，子弹与1的动量守恒，由动量守恒定律，并结合条件求出子弹射穿1后两者的速度．子弹穿过2时，子弹与2动量守恒，求出
子弹射穿2后两者的速度．接下来，弹簧开始被压缩，由于弹簧的弹力，1将做减速运动，2将做加速运动，当两者速度相等时，弹簧压缩量最大，弹性势能最大，由系统的动量守恒和机械能守恒列式求解
解答 解：子弹穿过1时，子弹与1动量守恒，由动量守恒定律：mv0=m1v1+mv′…①
而由v′=$\frac{3}{5}{v}_{0}$
得：v′=300m/s
得：v1=10m/s…②
子弹穿过2时，子弹与2动量守恒，由动量守恒定律：mv′=m2v2+mv″…③
又由$\frac{1}{2}m{{v}_{0}}^{2}-\frac{1}{2}mv{′}^{2}=2（\frac{1}{2}mv{′}^{2}-\frac{1}{2}mv{″}^{2}）$…④
得：v″=100m/s
由③，④得：v2=2.5m/s…⑤
子弹穿过2以后，弹簧开始被压缩，1、2和弹簧所组成的系统动量守恒，由动量守恒定律：m1v1+m2v2=（m1+m2）v共…⑥
由能量关系：Ep=$\frac{1}{2}{m}_{1}{{v}_{1}}^{2}+\frac{1}{2}{m}_{2}{{v}_{2}}^{2}-\frac{1}{2}（{m}_{1}+{m}_{2}）{{v}_{共}}^{2}$…⑦
由②⑤⑥⑦得：EP=22.5J…⑧
答：系统运动过程中弹簧的最大弹性势能为22.5J
点评 本题是含有弹簧的类型，对于子弹打击过程，要明确研究对象，确定哪些物体参与作用，运用动量守恒和机械能守恒进行求解即可．
练习册系列答案
名校课堂系列答案
相关题目
如图所示，足够长的木板静止在光滑的水平面上，距木板右端处有一固定挡板，一小物块从木板右端以初速度v0滑上木板，已知物块的质量为m，木板的质量为2m，木板与挡板碰撞无机械能的损失，物块不会从木板表面滑出，物块与木板间的动摩擦因数为μ，求：
如图所示，一个质量为m，电荷量为q的正离子，在D处沿图示方向以一定的速度射入磁感应强度为B的匀强磁场中，此磁场方向是垂直纸面向里．结果离子正好从距A点为d的小孔C沿垂直于电场方向进入匀强电场，此电场方向与AC平行且向上，最后离子打在G处，而G处距A点4d（AG⊥AC）．不计离子重力，离子运动轨迹在纸面内．求：
17．（2）某研究性学习小组利用伏安法测定某一电池组的电动势和内阻，实验原理如图甲所示，其中，虚线框内为用灵敏电流计G改装的电流表A，V为标准电压表，E为待测电池组，S为开关，R为滑动变阻器，R0是标称值为4.0Ω的定值电阻．
①已知灵敏电流计G的满偏电流Ig=100μA、内阻rg=2.0kΩ，若要改装后的电流表满偏电流为200mA，应并联一只1.0Ω（保留一位小数）的定值电阻R1；
②根据图甲，用笔画线代替导线将图乙连接成完整电路；
③某次试验的数据如表所示：该小组借鉴“研究匀变速直线运动”试验中计算加速度的方法（逐差法），计算出电池组的内阻r=1.66Ω（保留两位小数）；为减小偶然误差，逐差法在数据处理方面体现出的主要优点是充分利用已获得的数据．
①已知灵敏电流计G的满偏电流Ig=100μA、内阻rg=2.0kΩ，若要改装后的电流表满偏电流为200mA，应并联一只1.0Ω（保留一位小数）的定值电阻R1；
②根据图甲，用笔画线代替导线将图乙连接成完整电路；
③某次试验的数据如表所示：该小组借鉴“研究匀变速直线运动”试验中计算加速度的方法（逐差法），计算出电池组的内阻r=1.66Ω（保留两位小数）；为减小偶然误差，逐差法在数据处理方面体现出的主要优点是充分利用已获得的数据．
| 测量次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 电压表V读数U/V | 5.26 | 5.16 | 5.04 | 4.94 | 4.83 | 4.71 | 4.59 | 4.46 |
| 改装表A读数I/mA | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
在同一水平面中的光滑平行导轨P、Q相距L=1m，导轨左端接有如图所示的电路．其中水平放置的平行板电容器两极板M、N间距离d=10mm，定值电阻R1=R2=12Ω，R3=2Ω，金属棒ab电阻r=2Ω，其它电阻不计．磁感应强度B=1T的匀强磁场竖直穿过导轨平面，当金属棒ab沿导轨向右匀速运动时，悬浮于电容器两极板之间，质量m=1×10-14kg，带电量q=-1×10-14C的微粒恰好静止不动．取g=10m/s2，在整个运动过程中金属棒与导轨接触良好．且运动速度保持恒定．试求：
18．关于匀速圆周运动，下列说法正确的是（ ）
| A． | 匀速圆周运动是匀加速运动 | |
| B． | 做匀速圆周运动的物体处于平衡状态 | |
| C． | 匀速圆周运动是线速度不变的运动 | |
| D． | 匀速圆周运动是角速度不变的运动 |
