题目内容
17.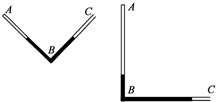 如图,竖直平面内有一直角形内径相同的细玻璃管,A端封闭,C端开口,AB=BC=l0,且此时A、C端等高.平衡时,管内水银总长度为l0,玻璃管AB内封闭有长为$\frac{{l}_{0}}{2}$的空气柱.已知大气压强为l0汞柱高.如果使玻璃管绕B点在竖直平面内顺时针缓慢地转动至BC管水平,求此时AB管内气体的压强为多少汞柱高?(管内封入的气体可视为理想气体且温度不变.)
如图,竖直平面内有一直角形内径相同的细玻璃管,A端封闭,C端开口,AB=BC=l0,且此时A、C端等高.平衡时,管内水银总长度为l0,玻璃管AB内封闭有长为$\frac{{l}_{0}}{2}$的空气柱.已知大气压强为l0汞柱高.如果使玻璃管绕B点在竖直平面内顺时针缓慢地转动至BC管水平,求此时AB管内气体的压强为多少汞柱高?(管内封入的气体可视为理想气体且温度不变.)
分析 找出封闭气体初末状态的气压和体积中的已知量,然后根据玻意耳定律列式求解.
解答 解:因BC长度为l0,故顺时针旋转至BC水平方向时水银未流出.
设A端空气柱此时长为x,管内横截面积为S,对A内气体:
P1=l0,V1=$\frac{l0}{2}$•S
P2=l0-(l0-x)=x,V2=x•S
对A中密闭气体,由玻意耳定律得:l0$\frac{l0}{2}$•S=x•xS,
解得:x=$\frac{\sqrt{2}}{2}$l0,即:P2=$\frac{\sqrt{2}}{2}$l0Hg;
答:此时AB管内气体的压强为$\frac{\sqrt{2}}{2}$l0Hg.
点评 本题考查了求其他的压强,分析清楚其他状态变化过程、求出气体的状态参量是 解题的前提与关键,应用玻意耳定律可以解题.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
8.甲、乙两人发生口角,甲打了乙的胸口一拳致使乙受伤,法院判决甲应支付乙的医疗费.甲狡辩说:我打了乙一拳,根据牛顿第三定律,作用力与反作用力大小相等,乙对我也有相同大小的作用力,所以乙并没有吃亏.那么这一事件判决的依据在哪里( )
| A. | 甲打乙的力大于乙对甲的作用力,判决甲付给乙的医疗费 | |
| B. | 甲打乙的力大小等于乙对甲的作用力,但拳头的承受力大于胸口的承受力,所以乙受伤而甲未受伤,甲又主动打乙,故判决甲支付乙的医疗费 | |
| C. | 甲打乙的力大小等于乙对甲的作用力,甲的拳和乙的胸受伤的程度不同,甲轻而乙重,故判决甲支付乙的医疗费 | |
| D. | 由于是甲用拳打乙的胸,所以甲对乙的力远大于乙胸对甲拳的作用力,故判决甲支付乙的医疗费 |
12.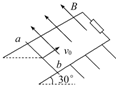 一质量为m、电阻为r的金属杆ab,以一定的初速度v0从一光滑平行金属导轨底端向上滑行,导轨平面与水平面成30°角,两导轨上端用一电阻R相连,如图所示,磁场垂直斜面向上,导轨的电阻不计,金属杆向上滑行到某一高度之后又返回到底端时的速度大小为v,则( )
一质量为m、电阻为r的金属杆ab,以一定的初速度v0从一光滑平行金属导轨底端向上滑行,导轨平面与水平面成30°角,两导轨上端用一电阻R相连,如图所示,磁场垂直斜面向上,导轨的电阻不计,金属杆向上滑行到某一高度之后又返回到底端时的速度大小为v,则( )
 一质量为m、电阻为r的金属杆ab,以一定的初速度v0从一光滑平行金属导轨底端向上滑行,导轨平面与水平面成30°角,两导轨上端用一电阻R相连,如图所示,磁场垂直斜面向上,导轨的电阻不计,金属杆向上滑行到某一高度之后又返回到底端时的速度大小为v,则( )
一质量为m、电阻为r的金属杆ab,以一定的初速度v0从一光滑平行金属导轨底端向上滑行,导轨平面与水平面成30°角,两导轨上端用一电阻R相连,如图所示,磁场垂直斜面向上,导轨的电阻不计,金属杆向上滑行到某一高度之后又返回到底端时的速度大小为v,则( )| A. | 向上滑行的时间大于向下滑行的时间 | |
| B. | 在向上滑行时电阻R上产生的热量小于向下滑行时电阻R上产生的热量 | |
| C. | 向上滑行时与向下滑行时通过电阻R的电荷量相等 | |
| D. | 金属杆从开始上滑至返回出发点,电阻R上产生的热量为$\frac{1}{2}$m(v02-v2) |
9.关于放射性元素,下列说法正确的是( )
| A. | 利用放射性同位素可作为示踪原子 | |
| B. | 利用放射性同位素放出的α射线可以进行金属探伤 | |
| C. | 放射性元素发生一次β衰变,质子数减少1 | |
| D. | 放射性元素的半衰期随环境温度的升高而缩短 |
6. 如图所示,某人静躺在椅子上,椅子的靠背与水平面之间有固定倾斜角θ.若此人所受重力为G,则椅子各部分对他的作用力的合力大小为( )
如图所示,某人静躺在椅子上,椅子的靠背与水平面之间有固定倾斜角θ.若此人所受重力为G,则椅子各部分对他的作用力的合力大小为( )
 如图所示,某人静躺在椅子上,椅子的靠背与水平面之间有固定倾斜角θ.若此人所受重力为G,则椅子各部分对他的作用力的合力大小为( )
如图所示,某人静躺在椅子上,椅子的靠背与水平面之间有固定倾斜角θ.若此人所受重力为G,则椅子各部分对他的作用力的合力大小为( )| A. | G | B. | Gsin θ | C. | Gcos θ | D. | Gtan θ |
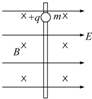 如图所示,在互相垂直的水平方向的匀强电场(E已知)和匀强磁场(B已知)中,有一固定的竖直绝缘杆,杆上套有一个质量为m、电荷量为+q的小球,它们之间的动摩擦因数为μ.现由静止释放小球,则小球下落的最大速度vm=$\frac{mg-μqE}{μqB}$.(mg>μqE)
如图所示,在互相垂直的水平方向的匀强电场(E已知)和匀强磁场(B已知)中,有一固定的竖直绝缘杆,杆上套有一个质量为m、电荷量为+q的小球,它们之间的动摩擦因数为μ.现由静止释放小球,则小球下落的最大速度vm=$\frac{mg-μqE}{μqB}$.(mg>μqE)