题目内容
16.一质量为m的物块从某高处以速度v0水平抛出,在抛出点其动能为重力势能的3倍,取水平地面为重力势能的参考平面,不计空气阻力,则以下结论正确的是( )| A. | 物块落地时的速度方向与水平方向的夹角为$\frac{π}{6}$ | |
| B. | 物块落地时的速度方向与水平方向的夹角为$\frac{π}{3}$ | |
| C. | 下落过程中重力的冲量大小为$\frac{\sqrt{3}m{v}_{0}}{3}$ | |
| D. | 下落过程中重力的冲量大小为$\frac{2\sqrt{3}m{v}_{0}}{3}$ |
分析 根据机械能守恒定律,以及已知条件:抛出时动能恰好是重力势能的3倍,分别列式即可求出落地时速度与水平速度的关系,从而求出物块落地时的速度方向与水平方向的夹角,根据动量定理求解下落过程中重力的冲量.
解答 解:AB、设抛出时物体的初速度为v0,高度为h,物块落地时的速度大小为v,方向与水平方向的夹角为α.
根据机械能守恒定律得:$\frac{1}{2}$m${{v}_{0}}^{2}$+mgh=$\frac{1}{2}$mv2
据题有:$\frac{1}{2}$m${{v}_{0}}^{2}$=3mgh
联立解得:$v=\frac{2\sqrt{3}}{3}$v0;
则 cosα=$\frac{{v}_{0}}{v}=\frac{\sqrt{3}}{2}$
可得 α=$\frac{π}{6}$,故A正确,B错误;
CD、末位置竖直方向的速度为:${v}_{y}={v}_{0}tan\frac{π}{6}=\frac{\sqrt{3}}{3}{v}_{0}$,根据动量定理得下落过程中重力的冲量大小为:I=$m{v}_{y}=\frac{\sqrt{3}m{v}_{0}}{3}$,故C正确,D错误.
故选:AC
点评 解决本题的关键会熟练运用机械能守恒定律处理平抛运动,并要掌握平抛运动的研究方法:运动的分解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.利用如图所示的实验装置做“研究平抛运动”的实验时,为减小误差,应采取的措施是( )


| A. | 斜槽轨道必须光滑 | |
| B. | 斜槽水平轨道必须水平 | |
| C. | 用密度比较大的小球 | |
| D. | 小球从斜槽上释放的高度要逐渐降低 |
4. 有三个完全相同的金属小球A、B、C,其中小球C不带电,小球A和B带有等量的同种电荷,如图所示,A球固定在竖直支架上,B球用不可伸长的绝缘细线悬于A球正上方的P点处,静止时细线与OA的夹角为θ.小球C可用绝缘手柄移动,重力加速度为g,现在进行下列操作,其中描述与事实相符的是( )
有三个完全相同的金属小球A、B、C,其中小球C不带电,小球A和B带有等量的同种电荷,如图所示,A球固定在竖直支架上,B球用不可伸长的绝缘细线悬于A球正上方的P点处,静止时细线与OA的夹角为θ.小球C可用绝缘手柄移动,重力加速度为g,现在进行下列操作,其中描述与事实相符的是( )
 有三个完全相同的金属小球A、B、C,其中小球C不带电,小球A和B带有等量的同种电荷,如图所示,A球固定在竖直支架上,B球用不可伸长的绝缘细线悬于A球正上方的P点处,静止时细线与OA的夹角为θ.小球C可用绝缘手柄移动,重力加速度为g,现在进行下列操作,其中描述与事实相符的是( )
有三个完全相同的金属小球A、B、C,其中小球C不带电,小球A和B带有等量的同种电荷,如图所示,A球固定在竖直支架上,B球用不可伸长的绝缘细线悬于A球正上方的P点处,静止时细线与OA的夹角为θ.小球C可用绝缘手柄移动,重力加速度为g,现在进行下列操作,其中描述与事实相符的是( )| A. | 仅将球C与球A接触离开后,B球再次静止时细线中的张力比原来要小 | |
| B. | 仅将球C与球A接触离开后,B球再次静止时细线与OA的夹角为θ1,仅将球C与球A接触离开后,B球再次静止时细线与OA的夹角为θ2,则θ1=θ2 | |
| C. | 剪断细线OB瞬间,球B的加速度等于g | |
| D. | 剪断细线OB后,球B将沿OB方向做匀变速直线运动直至着地 |
11.一质量为m的质点以速度v0匀速直线运动,在t=0时开始受到恒力F作用,速度大小先减小后增大,其最小值为v=0.5v0,由此可判断( )
| A. | 质点受力F作用后一定做匀变速曲线运动 | |
| B. | 质点受力F作用后可能做圆周运动 | |
| C. | t=0时恒力F与速度v0方向间的夹角为60° | |
| D. | t=$\frac{\sqrt{3}m{v}_{0}}{2F}$时,质点速度最小 |
1.下列各图为电流产生磁场的磁感线示意图,其中正确的是( )


| A. | ①③ | B. | ②③ | C. | ①④ | D. | ②④ |
8. 如图所示,中间有孔的物块A套在光滑的竖直杆上,通过滑轮用不可伸长的轻绳拉着物块匀速向上运动一小段距离,不计一切阻力,则关于拉力F的功率P、拉力F作用点向下移动的速度v.下列说法正确的是( )
如图所示,中间有孔的物块A套在光滑的竖直杆上,通过滑轮用不可伸长的轻绳拉着物块匀速向上运动一小段距离,不计一切阻力,则关于拉力F的功率P、拉力F作用点向下移动的速度v.下列说法正确的是( )
 如图所示,中间有孔的物块A套在光滑的竖直杆上,通过滑轮用不可伸长的轻绳拉着物块匀速向上运动一小段距离,不计一切阻力,则关于拉力F的功率P、拉力F作用点向下移动的速度v.下列说法正确的是( )
如图所示,中间有孔的物块A套在光滑的竖直杆上,通过滑轮用不可伸长的轻绳拉着物块匀速向上运动一小段距离,不计一切阻力,则关于拉力F的功率P、拉力F作用点向下移动的速度v.下列说法正确的是( )| A. | v减小 | B. | v增大 | C. | P减小 | D. | P增大 |
5.卫星发射时,可利用其随地球自转的速度,达到节省燃料的目的.仅从该角度考虑,卫星发射场的位置应建在( )
| A. | 赤道附近 | B. | 靠近南极 | C. | 靠近北极 | D. | 地面任意处 |
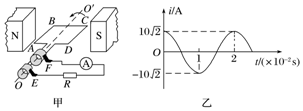
12.图甲是小型交流发电机的示意图,两磁极N、S间的磁场可视为水平方向的匀强磁场, 为交流电流表.线圈绕垂直于磁场的水平轴OO′沿逆时针方向匀速转动,从图甲所示位置开始计时,产生的交变电流随时间变化的图象如图乙所示.以下判断正确的是( )
为交流电流表.线圈绕垂直于磁场的水平轴OO′沿逆时针方向匀速转动,从图甲所示位置开始计时,产生的交变电流随时间变化的图象如图乙所示.以下判断正确的是( )
 为交流电流表.线圈绕垂直于磁场的水平轴OO′沿逆时针方向匀速转动,从图甲所示位置开始计时,产生的交变电流随时间变化的图象如图乙所示.以下判断正确的是( )
为交流电流表.线圈绕垂直于磁场的水平轴OO′沿逆时针方向匀速转动,从图甲所示位置开始计时,产生的交变电流随时间变化的图象如图乙所示.以下判断正确的是( )
| A. | 线圈转动的角速度为50π rad/s | |
| B. | 电流表的示数为10A | |
| C. | t=0.01s时,线圈平面与磁场方向平行 | |
| D. | t=0.02s时,电阻R中电流的方向自右向左 |
 为了将物体从小山坡的A端运送到D端,设计了如图所示的传送皮带,其左边倾斜部分AB的长度为20m,AB与水平面的夹角为α=37°,水平部分BC的长度为16.25m,右边倾斜部分CD的长度为16.875m,CD与水平面的夹角为θ=53°.将一物体(可视为质点)轻轻放于A端的传送带上,物体与传送带间的动摩擦因数为μ=0.8.传送带沿图示方向以v=6m/s的速度匀速运动,若物体始终未脱离皮带,试求物体从A端被传送到D端所用的时间.(g=10m/s2,sin37°=0.6,cos37°=0.8,sin53°=0.8,cos53°=0.6)
为了将物体从小山坡的A端运送到D端,设计了如图所示的传送皮带,其左边倾斜部分AB的长度为20m,AB与水平面的夹角为α=37°,水平部分BC的长度为16.25m,右边倾斜部分CD的长度为16.875m,CD与水平面的夹角为θ=53°.将一物体(可视为质点)轻轻放于A端的传送带上,物体与传送带间的动摩擦因数为μ=0.8.传送带沿图示方向以v=6m/s的速度匀速运动,若物体始终未脱离皮带,试求物体从A端被传送到D端所用的时间.(g=10m/s2,sin37°=0.6,cos37°=0.8,sin53°=0.8,cos53°=0.6)