题目内容
2011年11月3日,“神州八号”飞船与“天宫一号”目标飞行器成功实施了首次交会对接。任务完成后“天宫一号”经变轨升到更高的轨道,等待与“神州九号”第二次交会对接.变轨前和变轨完成后“天宫一号”的运行轨道均可视为圆轨道,对应的轨道半径分别为 、
、 ,对应的角速度和向心加速度分别为
,对应的角速度和向心加速度分别为 、
、 和
和 、
、 ,则有( )
,则有( )
A. |
B. |
| C.变轨后的“天宫一号”比变轨前动能增大了,机械能增加了 |
| D.在正常运行的“天宫一号”内,体重计、弹簧测力计、天平都不能使用了 |
B
解析试题分析:对绕地球运行的卫星,由万有引力提供圆周运动的向心力有: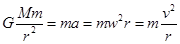 , 由
, 由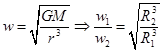 ,故A错误。由
,故A错误。由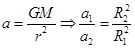 ,故B正确。卫星由
,故B正确。卫星由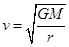 ,轨道半径增加,卫星运行线速度减小,动能减小,故C错误。弹簧测力计是利用胡克定律
,轨道半径增加,卫星运行线速度减小,动能减小,故C错误。弹簧测力计是利用胡克定律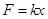 制作的,在失重的环境下仍可以使用,故D错误。故选B。
制作的,在失重的环境下仍可以使用,故D错误。故选B。
考点:本题考查了万有引力定律、卫星的运动规律、卫星变轨、机械能守恒定律。

右图是“牛顿摆”装置,5个完全相同的小钢球用轻绳悬挂在水平支架上,5根轻绳互相平行,5个钢球彼此紧密排列,球心等高。用1、2、3、4、5分别标记5个小钢球。当把小球1向左拉起一定高度,如图甲所示,然后由静止释放,在极短时间内经过小球间的相互碰撞,可观察到球5向右摆起,且达到的最大高度与球1的释放高度相同,如图乙所示。关于此实验,下列说法中正确的是

| A.上述实验过程中,5个小球组成的系统机械能守恒,动量守恒 |
| B.上述实验过程中,5个小球组成的系统机械能不守恒,动量不守恒 |
| C.如果同时向左拉起小球1、2、3到相同高度(如图丙所示),同时由静止释放,经碰撞后,小球4、5一起向右摆起,且上升的最大高度高于小球1、2、3的释放高度 |
| D.如果同时向左拉起小球1、2、3到相同高度(如图丙所示),同时由静止释放,经碰撞后,小球3、4、5一起向右摆起,且上升的最大高度与小球1、2、3的释放高度相同 |
如图所示,在地面上以速度v0抛出质量为m的物体,抛出后物体落到比地面低h的海平面上.若以地面为零势能面而且不计空气阻力,则
①物体到海平面时的势能为mgh ②重力对物体做的功为mgh
③物体在海平面上的动能为 mv02+mgh ④物体在海平面上的机械能为
mv02+mgh ④物体在海平面上的机械能为 mv02
mv02
其中正确的是( )
| A.①②③ | B.②③④ | C.①③④ | D.①②④ |
如图所示,一物体以初速度v0冲向光滑斜面AB,并恰好能沿斜面升高h,下列说法中正确的是( )
| A.若把斜面从C点锯断,物体冲过C点后仍升高h |
| B.若把斜面弯成圆弧形D,物体仍沿圆弧升高h |
| C.若把斜面从C点锯断或弯成圆弧状,物体都不能升高h |
| D.若把斜面AB变成曲面AEB,物体沿此曲面上升仍能到B点 |
如图所示,两个3/4圆弧轨道固定在水平地面上,半径R相同,A轨道由金属凹槽制成,B轨道由金属圆管制成,均可视为光滑轨道。在两轨道右侧的正上方分别将金属小球A和B由静止释放,小球距离地面的高度分别用hA和hB表示,对于下述说法中正确的是
| A.若hA=hB ≥2R,则两小球都能沿轨道运动到最高点 |
| B.若hA=hB=3R/2,由于机械能守恒,两小球在轨道上上升的最大高度均为3R/2 |
| C.适当调整hA,,可使A小球从轨道最高点飞出后再次进入圆形轨道运动 |
| D.适当调整hB,可使B小球从轨道最高点飞出后再次进入圆形轨道运动 |
如图,倾角为 的斜面体放在粗糙的水平面上,质量为m的物体A与一劲度系数为k的轻弹簧相连.现用拉力F沿斜面向上拉弹簧,使物体A在光滑斜面上匀速上滑,上滑的高度为h,斜面体始终处于静止状态。在这一过程中
的斜面体放在粗糙的水平面上,质量为m的物体A与一劲度系数为k的轻弹簧相连.现用拉力F沿斜面向上拉弹簧,使物体A在光滑斜面上匀速上滑,上滑的高度为h,斜面体始终处于静止状态。在这一过程中
A.弹簧的伸长量为 |
B.拉力F做的功为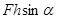 |
| C.物体A 的机械能增加mgh |
D.斜面体受地面的静摩擦力大小等于Fcos |
下列说法正确的是 ( )
| A.如果物体(或系统)所受到的合外力为零,则机械能一定守恒 |
| B.如果合外力对物体(或系统)做功为零,则机械能一定守恒 |
| C.物体沿光滑曲面自由下滑过程中,机械能一定守恒 |
| D.做匀加速运动的物体,其机械能一定不守恒 |
如图所示为某探究活动小组设计的节能运输系统.斜面轨道倾角为30°,质量为M的木箱与轨道的动摩擦因数为 =
=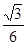 .木箱在轨道顶端时,自动装货装置将质量为m的货物装入木箱,然后木箱载着货物沿轨道无初速滑下,与轻弹簧被压缩至最短时,自动卸货装置立刻将货物卸下,然后木箱恰好被弹回到轨道顶端,再重复上述过程.下列选项正确的是( )
.木箱在轨道顶端时,自动装货装置将质量为m的货物装入木箱,然后木箱载着货物沿轨道无初速滑下,与轻弹簧被压缩至最短时,自动卸货装置立刻将货物卸下,然后木箱恰好被弹回到轨道顶端,再重复上述过程.下列选项正确的是( )
| A.木箱与弹簧接触时速度达到最大 |
| B.货物的质量m等于木箱质量M的2倍 |
| C.木箱不与弹簧接触时,上滑的加速度小于下滑的加速度 |
| D.在木箱与货物从顶端滑到最低点的过程中,减少的重力势能大于弹簧的弹性势能 |




