题目内容
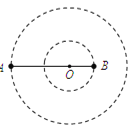
【题目】如图，质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速周运动，星球A和B两者中心之间距离为L.已知A、B的中心和O三点始终共线，A和B分别在O的两侧.引力常数为G.
（1）求两星球做圆周运动的周期T；
（2）在地月系统中，若忽略其它星球的影响，可以将月球和地球看成上述星球A和B，月球绕其轨道中心运行的周期记为T1.但在近似处理问题时，常常认为月球是绕地心做圆周运动的，这样算得的运行周期T2.已知地球和月球的质量分别为5.98×1021kg和7.35×1022kg.求T2与T1两者平方之比.(结果保留2位小数)
【答案】（1）
；（2）
；
【解析】(1)设两个星球A和B做匀速圆周运动的轨道半径分别为r和R，相互作用的万有引力大小为F，运行周期为T.根据万有引力定律有: 
①
由匀速圆周运动的规律得
②
③
根据题意有L=R+r ④
联立①②③④式得:T=
⑤
(2)在地月系统中，因为地月系统旋转所围绕的中心O不在地心，根据题意知，月球做圆周运动的周期可由⑤式得出
⑥
式中，M'和m'分别是地球与月球的质量，L'是地心与月心之间的距离.若认为月球在地球的引力作用下绕地心做匀速圆周运动，则
⑦
式中，T2为月球绕地心运动的周期.由⑦式得: 
⑧
由⑥⑧式得:
⑨
代入题给数据得:
⑩.
练习册系列答案
快捷英语周周练系列答案
相关题目
