题目内容
【题目】如图所示,倾角为θ的斜面上有B、C两点,在B点竖直地固定一光滑直杆AB,AB=BC=s.A点与斜面底端C点间置有一光滑的直杆AC.两杆上各穿有一钢球(视为质点).将两球从A点同时由静止释放,分别沿两细杆滑到杆的末端.球由A到B的时间t1 , 球由A到C的时间t2 . 不计一切阻力影响,则下列说法正确的是( )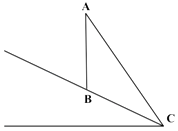
A.条件不足,无法判断两球运动时间关系
B.t1=t2
C.球由A到B的时间与球由A到C的时间之比为1: ![]()
D.球由A到B的时间与球由A到C的时间之比为1:( ![]() +1)
+1)
【答案】C
【解析】解:质点沿AB杆下滑的加速度 a=g,位移 x=s,由x= ![]() 可得:t1=
可得:t1= ![]() ;
;
质点沿AC杆下滑,令∠BAC=α,则位移 x′=2scosα,加速度为:a′= ![]() =gcosα
=gcosα
根据位移时间关系有 x′= ![]()
可得运动时间为:t2= ![]()
所以可得 t1:t2=1: ![]()
故选:C
【考点精析】通过灵活运用匀变速直线运动的速度、位移、时间的关系,掌握速度公式:V=V0+at;位移公式:s=v0t+1/2at2;速度位移公式:vt2-v02=2as;以上各式均为矢量式,应用时应规定正方向,然后把矢量化为代数量求解,通常选初速度方向为正方向,凡是跟正方向一致的取“+”值,跟正方向相反的取“-”值即可以解答此题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目