��Ŀ����
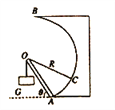
����Ŀ����ͼ�Ƿ�����ɽ����ģ�ͣ��⻬����ֱԲ����뾶ΪR=2m����ڵ�ƽֱ���AC�ͳ��ڵ�ƽֱ���CD���Ǵֲڵģ�����Ϊm=2kg��С����ˮƽ���֮��Ķ�Ħ�����ؾ�Ϊ��=0.5�����ٽ�AB�ij���Ϊl=3m��С������A��ֹ��ʼ�ܵ�ˮƽ����F=60N�����ã���B�㳷ȥ���������ʣ�
��1��ҪʹС��ǡ��ͨ��Բ�������ߵ㣬С����C����ٶ�Ϊ���٣�
��2������ڣ�1���������£�С�����ų���ƽ���CD���ж�Զ�ľ��룿
��3��ҪʹС������������ƽֱ���BC�εij��ȷ�Χ��
���𰸡�
��1��
�⣺ҪʹС��ͨ����ߵ㣬���У�
mg=m ![]()
��ã�v= ![]() =
= ![]() m/s��
m/s��
��CD�����ɻ�е���غ㶨�ɿɵã�
mg2R= ![]() ��
�� ![]() mv2
mv2
��ã�vc=10m/s
��2��
�⣺��С���C�㵽���ֹͣ�����ɶ��ܶ����ɵã�
����mgx=0�� ![]() mvc2
mvc2
��ã�x= ![]() ��
�� ![]() =
= ![]() =10m
=10m
��3��
�⣺ҪʹС�����������������ֿ��ܣ�
�١�С����ͨ����ߵ㣬������C����ٶȴ���10m/s��
���AC�����ɶ��ܶ����ɵã�
Fl����mg��l+x1��= ![]() mv2��
mv2��
��ã�x1=5m��
Ҫʹ��ͨ����ߵ㣬x1ӦС��5m��
�ڡ�С����ͨ����ߵ㣬������ĸ߶�ΪRʱ�ٶ�Ϊ�㣬С��ͬ��������������
���ȫ���ɶ��ܶ����ɵã�
Fl����mg��l+x2����mgR=0
��ã�x2=11m��
��Ҫʹ��������BC���ȿ���С��5m�����11m
����������1�������������������������ߵ���ٶȣ����ɻ�е���غ㶨�ɿ����C����ٶȣ���2����C��ֹͣ�����ɶ��ܶ��������С���еľ��룻��3������С����ܵ��˶�������ɶ��ܶ������з�����ȷλ�Ʒ�Χ��
�����㾫����ͨ�������������������������������ָ��Բ�ģ��������ļ��ٶȣ�������ֻ�ı����ٶȵķ����ı��ٶȵĴ�С���������Ǹ�������Ч��������.�ڷ�����Բ���˶����ʵ��������ʱ��ǧ������������֮��������һ�������������Խ����⣮

 ����ѧ���ʱѧ����ϵ�д�
����ѧ���ʱѧ����ϵ�д� �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д�