题目内容
如图所示,在xoy 坐标平面的第一象限内有一沿y 轴正方向的匀强电场,在第四象限内有一垂直于平面向内的匀强磁场,现有一质量为m 带电量为q的负粒子(重力不计)从电场中坐标为(3L,L)的P点与x轴负方向相同的速度v0射入,在x轴上的Q点进入磁场,进入磁场速度方向与x轴负方向成45°夹角,然后粒子恰好能从O点射出,求:粒子在O点的速度大小。
求:
(1)粒子在O点的速度大小;
(2)匀强电场的场强E;
(3)粒子从P点运动到O点所用的时间。

求:
(1)粒子在O点的速度大小;
(2)匀强电场的场强E;
(3)粒子从P点运动到O点所用的时间。

(1)粒子运动轨迹如图所示,设粒子在P点时速度大小为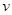 ,OQ段为四分之一圆弧,QP段为抛物线,根据对称性可知,粒子在Q点的速度大小也为
,OQ段为四分之一圆弧,QP段为抛物线,根据对称性可知,粒子在Q点的速度大小也为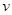 ,方向与x轴正方向成450.
,方向与x轴正方向成450.
可得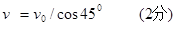
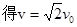 (1分)
(1分)
(2)Q到P过程,由动能定理得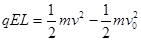 (3分)
(3分)
即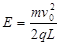 (1分)
(1分)
(3)在Q点时,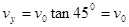 (1分)
(1分)
由P到Q过程中, 竖直方向上有: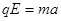 (1分)
(1分)
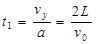 (2分)
(2分)
水平方向有: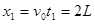 (1分)
(1分)
则OQ=3L-2L=L (1分)
得粒子在OQ段圆周运动的半径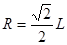 (2分)
(2分)
Q到O的时间: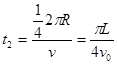 (2分)
(2分)
粒子从P到O点所用的时间:t=t1+t2=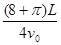
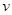 ,OQ段为四分之一圆弧,QP段为抛物线,根据对称性可知,粒子在Q点的速度大小也为
,OQ段为四分之一圆弧,QP段为抛物线,根据对称性可知,粒子在Q点的速度大小也为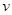 ,方向与x轴正方向成450.
,方向与x轴正方向成450.可得
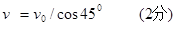
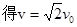 (1分)
(1分)(2)Q到P过程,由动能定理得
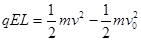 (3分)
(3分) 即
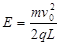 (1分)
(1分)(3)在Q点时,
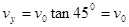 (1分)
(1分)由P到Q过程中, 竖直方向上有:
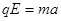 (1分)
(1分) 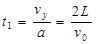 (2分)
(2分)水平方向有:
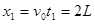 (1分)
(1分) 则OQ=3L-2L=L (1分)
得粒子在OQ段圆周运动的半径
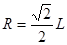 (2分)
(2分)Q到O的时间:
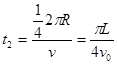 (2分)
(2分)粒子从P到O点所用的时间:t=t1+t2=
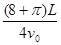
(1)粒子运动轨迹如图所示,设粒子在P点时速度大小为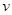 ,OQ段为四分之一圆弧,QP段为抛物线,根据对称性可知,粒子在Q点的速度大小也为
,OQ段为四分之一圆弧,QP段为抛物线,根据对称性可知,粒子在Q点的速度大小也为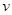 ,方向与x轴正方向成450.
,方向与x轴正方向成450.
可得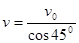
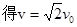
(2)Q到P过程,由动能定理得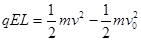 ,即
,即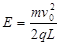
(3)在Q点时,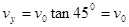 ,由P到Q过程中, 竖直方向上有:
,由P到Q过程中, 竖直方向上有: 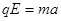
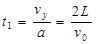 ,水平方向有:
,水平方向有: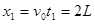 ,则OQ="3L-2L=L" ,
,则OQ="3L-2L=L" ,
得粒子在OQ段圆周运动的半径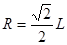 ,Q到O的时间:
,Q到O的时间: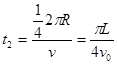
粒子从P到O点所用的时间:t=t1+t2=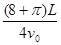
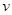 ,OQ段为四分之一圆弧,QP段为抛物线,根据对称性可知,粒子在Q点的速度大小也为
,OQ段为四分之一圆弧,QP段为抛物线,根据对称性可知,粒子在Q点的速度大小也为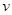 ,方向与x轴正方向成450.
,方向与x轴正方向成450.可得
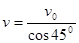
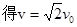
(2)Q到P过程,由动能定理得
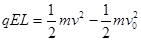 ,即
,即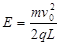
(3)在Q点时,
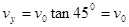 ,由P到Q过程中, 竖直方向上有:
,由P到Q过程中, 竖直方向上有: 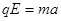
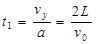 ,水平方向有:
,水平方向有: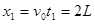 ,则OQ="3L-2L=L" ,
,则OQ="3L-2L=L" ,得粒子在OQ段圆周运动的半径
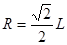 ,Q到O的时间:
,Q到O的时间: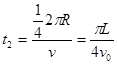
粒子从P到O点所用的时间:t=t1+t2=
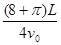

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 的低速质子,另一部分为速度大小为3
的低速质子,另一部分为速度大小为3
 穿过磁场Ⅰ后进入右边磁场Ⅱ并按某一路径再返回到磁场Ⅰ的边界MN上的某一点b(图中末画出),(途中虚线为磁场区域的分界面)求:
穿过磁场Ⅰ后进入右边磁场Ⅱ并按某一路径再返回到磁场Ⅰ的边界MN上的某一点b(图中末画出),(途中虚线为磁场区域的分界面)求:
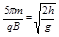 ,则小球落点与抛出点A的水平位移S是 ( )
,则小球落点与抛出点A的水平位移S是 ( )
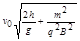
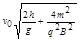
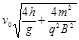
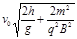

 的两块正对的平行金属板P、Q,板长
的两块正对的平行金属板P、Q,板长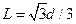 两板带等量异种电荷,上极板带负电。在MN右侧存在垂直于纸面的矩形匀强磁场(图中未画出),其左边界和下边界分别与MN、AA’重合(边界上有磁场)。现有一带电粒子以初速度v0沿两板中央OO′射入,并恰好从下极板边缘射出,又经过在矩形有界磁场中的偏转,最终垂直于MN从A点向左水平射出。 已知A点与下极板右端的距离为d。不计带电粒子重力。求:
两板带等量异种电荷,上极板带负电。在MN右侧存在垂直于纸面的矩形匀强磁场(图中未画出),其左边界和下边界分别与MN、AA’重合(边界上有磁场)。现有一带电粒子以初速度v0沿两板中央OO′射入,并恰好从下极板边缘射出,又经过在矩形有界磁场中的偏转,最终垂直于MN从A点向左水平射出。 已知A点与下极板右端的距离为d。不计带电粒子重力。求: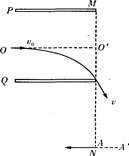

 0.6,cos37°=0.8,g=10m/s2)
0.6,cos37°=0.8,g=10m/s2)
