题目内容
(供选学物理3-1的考生做)(8分)在真空中有如图12所示的坐标系,坐标系中y>0的区域有垂直于xOy平面向里的匀强磁场,磁感应强度为B;y<0区域有沿y轴负方向的匀强电场,场强为E。一质量为m,电荷量为-q(q>0)的粒子从坐标原点O以初速度v0沿着y轴正方向射出。求:(1)粒子被射出后第一次通过x轴时,其与O的距离;(2)从粒子被射出到其第三次通过x轴的时间。(重力可忽略不计)。


(1)带电粒子在磁场中受洛仑兹力做匀速圆周运动,设其运动的半径为R,根据牛顿第二定律和洛仑兹力公式有qv0B=mv02/R …………………………………………(2分)
解得R=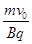 ……………………………………………………………………………(1分)
……………………………………………………………………………(1分)
粒子被射出后第一次通过x轴时恰好运动了半个圆周,所以其通过x轴时与O的距离为
x=2R=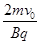 …………………………………………………………………………(1分)
…………………………………………………………………………(1分)
(2)带电粒子被射出后第一次通过x轴后进入电场中做匀变速直线运动,设其加速度为a,根据牛顿第二定律有 qE=ma,解得a=qE/m……………………………………(1分)
设粒子从第一次通过x轴至第二次通过x轴的时间(在电场中运动的时间)为t1,根据运动学公式有 0=v0t1-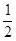 at12,解得t1=
at12,解得t1=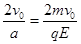 ……………………………………(1分)
……………………………………(1分)
粒子从电场中进入磁场中再次做匀速圆周运动,当完成半个圆周时第三次通过x轴。即粒子从射出后到第三次通过x轴的过程中,在磁场中做两次半个圆周运动。所以粒子在磁场中运动的时间t2=T=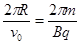 …………………………………………………………(1分)
…………………………………………………………(1分)
从粒子被射出到其第三次通过x轴的时间t= t1+ t2=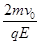 +
+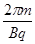 …………………(1分)
…………………(1分)
解得R=
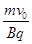 ……………………………………………………………………………(1分)
……………………………………………………………………………(1分)粒子被射出后第一次通过x轴时恰好运动了半个圆周,所以其通过x轴时与O的距离为
x=2R=
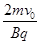 …………………………………………………………………………(1分)
…………………………………………………………………………(1分)(2)带电粒子被射出后第一次通过x轴后进入电场中做匀变速直线运动,设其加速度为a,根据牛顿第二定律有 qE=ma,解得a=qE/m……………………………………(1分)
设粒子从第一次通过x轴至第二次通过x轴的时间(在电场中运动的时间)为t1,根据运动学公式有 0=v0t1-
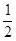 at12,解得t1=
at12,解得t1=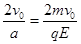 ……………………………………(1分)
……………………………………(1分)粒子从电场中进入磁场中再次做匀速圆周运动,当完成半个圆周时第三次通过x轴。即粒子从射出后到第三次通过x轴的过程中,在磁场中做两次半个圆周运动。所以粒子在磁场中运动的时间t2=T=
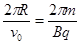 …………………………………………………………(1分)
…………………………………………………………(1分)从粒子被射出到其第三次通过x轴的时间t= t1+ t2=
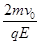 +
+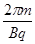 …………………(1分)
…………………(1分)(1)带电粒子在磁场中受洛仑兹力做匀速圆周运动,有qv0B=mv02/R ,解得R=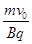
粒子被射出后第一次通过x轴时恰好运动了半个圆周,所以其通过x轴时与O的距离为,x=2R=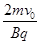
(2)带电粒子进入电场中做匀变速直线运动,根据牛顿第二定律有 qE=ma,解得a=qE/m,根据运动学公式有 0=v0t1-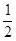 at12,解得t1=
at12,解得t1=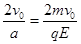 ,粒子从电场中进入磁场做匀速圆周运动,当完成半个圆周时第三次通过x轴,在磁场中做两次半个圆周运动。所以粒子在磁场中运动的时间t2=T=
,粒子从电场中进入磁场做匀速圆周运动,当完成半个圆周时第三次通过x轴,在磁场中做两次半个圆周运动。所以粒子在磁场中运动的时间t2=T=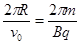 ,从粒子被射出到其第三次通过x轴的时间t= t1+ t2=
,从粒子被射出到其第三次通过x轴的时间t= t1+ t2=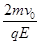 +
+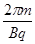
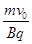
粒子被射出后第一次通过x轴时恰好运动了半个圆周,所以其通过x轴时与O的距离为,x=2R=
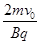
(2)带电粒子进入电场中做匀变速直线运动,根据牛顿第二定律有 qE=ma,解得a=qE/m,根据运动学公式有 0=v0t1-
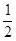 at12,解得t1=
at12,解得t1=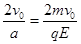 ,粒子从电场中进入磁场做匀速圆周运动,当完成半个圆周时第三次通过x轴,在磁场中做两次半个圆周运动。所以粒子在磁场中运动的时间t2=T=
,粒子从电场中进入磁场做匀速圆周运动,当完成半个圆周时第三次通过x轴,在磁场中做两次半个圆周运动。所以粒子在磁场中运动的时间t2=T=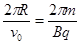 ,从粒子被射出到其第三次通过x轴的时间t= t1+ t2=
,从粒子被射出到其第三次通过x轴的时间t= t1+ t2=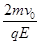 +
+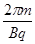

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案
相关题目
 角,整个装置处在与导轨平面垂直的匀强磁场中.现给导体棒沿导轨向上的初速度v0,经时间t0导体棒到达最高点,然后开始返回,到达底端前已经做匀速运动,速度大小为
角,整个装置处在与导轨平面垂直的匀强磁场中.现给导体棒沿导轨向上的初速度v0,经时间t0导体棒到达最高点,然后开始返回,到达底端前已经做匀速运动,速度大小为 .已知导体棒的电阻为R,其余电阻不计,重力加速度为g,忽略电路中感应电流之间的相互作用.求:
.已知导体棒的电阻为R,其余电阻不计,重力加速度为g,忽略电路中感应电流之间的相互作用.求:




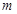 、带电量为q的液滴从p点沿图中虚线匀速运动到原点o进入第二象限,在第二象限内存在水平向右的匀强电场,其场强大小为E2。已知P点坐标为(4L,-3L),重力加速度为g。求:
、带电量为q的液滴从p点沿图中虚线匀速运动到原点o进入第二象限,在第二象限内存在水平向右的匀强电场,其场强大小为E2。已知P点坐标为(4L,-3L),重力加速度为g。求: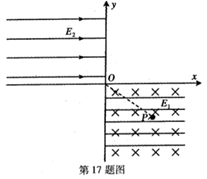
 轴时的坐标。
轴时的坐标。
