��Ŀ����
����Ŀ����ͼ����ʾ��С��B��ֹ�ڹ⻬ˮƽ���ϣ�һ������Ϊm������A������Ϊ�ʵ㣩����ˮƽ�ٶ�v0��4.0m/s����С��B����ˣ�Ȼ����С���ҵ�����ײ�����ǡ�û���С�����е㣬��֪![]() ��С�����泤L��1m����A�뵲����ײ��е����ʧ����ײʱ��ɺ��Բ��ƣ�gȡ10m/s2����
��С�����泤L��1m����A�뵲����ײ��е����ʧ����ײʱ��ɺ��Բ��ƣ�gȡ10m/s2����
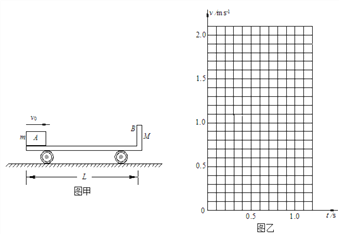
(1)A��B����ٶȵĴ�С��
(2)����A��С��B֮��Ķ�Ħ��������
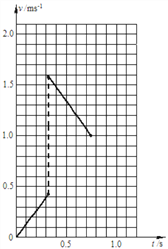
(3)����A��С��B�ĵ�������ײǰ��С��B���ٶȣ�����ͼ�ҵ������л���A��B��Ի���������С��B��Ե�����ٶ�v��tͼ�ߡ�
���𰸡�(1)v=1m/s (2)��=0.4 (3)0.423m/s ,1.577m/s
���������������������⻬��A��B��ɵ�ϵͳ�����غ㣬�ɶ����غ㶨�ɿ���������յ��ٶȣ���A��B��ɵ�ϵͳ���ɶ��ܶ����������A��B��Ķ�Ħ��������Ӧ�ö����غ㶨�ɡ������غ㶨�ɡ�ţ�ٵڶ����ɡ��˶�ѧ��ʽ���A��B���ٶȣ�Ȼ������ͼ��
��1����A��Bϵͳ���ɶ����غ㶨�ɣ�Mv0��(M��m)v
�ã�![]() ��
��
��2��A��Bϵͳ�����ܵ�ת�����غ㣬��ȫ������
![]()
�������ݽ�ã� ��=0.4
��3����A��B��ײǰ�ٶȷֱ�Ϊv10��v20��ϵͳ�����غ�
mv0=mv10+Mv20
��ϵͳ����ת�����غ�
![]()
���������������̣����
![]() (��
(��![]() ��
��
![]()
�ù���С��B���ȼ����˶�����mg=MaM
�������ݽ����![]()
![]()
�������ݽ����![]()
A��B������������A��B���ٶ�Ϊv1�� v2
A��B��ϵͳ�����غ��� mv0=mv1+Mv2
��ϵͳ��е���غ�
![]()
���������������̣����
![]() ����
����![]() ��
��
������˵����������
![]()
�ù���С��B���ȼ����˶�������mg=MaM
�������ݽ����![]()
��������Ծ�ֹ v�� v2��aMt2
�����t2=0.433 s
���ԣ��˶�����ʱ��Ϊt=t1+t2=0.75 s
С��B��v-tͼ����ͼ��ʾ��
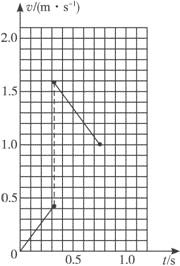

 ��ڽ��ȫ������ϵ�д�
��ڽ��ȫ������ϵ�д�