��Ŀ����
����Ŀ����18�֣���ͼ��ʾ������![]() ������
������![]() ������
������![]() �ĵ����
�ĵ����![]() �����U�ͽ�������ϡ��������
�����U�ͽ�������ϡ��������![]() �����ھ�Եˮƽ���ϣ���ˮƽ���Ķ�Ħ������
�����ھ�Եˮƽ���ϣ���ˮƽ���Ķ�Ħ������![]() �����0.4m��
�����0.4m��![]() ��
��![]() �ƽ�У����費�����㹻��������
�ƽ�У����費�����㹻��������![]() ��
��![]() ��ֱ��
��ֱ��![]() ������װ�ô�����ֱ���ϵ���ǿ�ų��У��Ÿ�Ӧǿ��
������װ�ô�����ֱ���ϵ���ǿ�ų��У��Ÿ�Ӧǿ��![]() ����ֱ��
����ֱ��![]() ʩ��
ʩ��![]() ��ˮƽ������
��ˮƽ������![]() �Ӿ�ֹ��ʼ��Ħ�����˶���ʼ����
�Ӿ�ֹ��ʼ��Ħ�����˶���ʼ����![]() ��
��![]() �������ýӴ�����
�������ýӴ�����![]() �˶���ij��ʱ����ܿ�ʼ�˶���������ˮƽ������Ħ�������ڻ���Ħ������gȡ10m/s2��
�˶���ij��ʱ����ܿ�ʼ�˶���������ˮƽ������Ħ�������ڻ���Ħ������gȡ10m/s2��
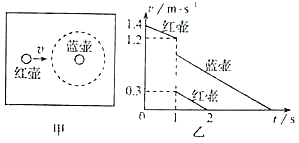
��1�����ܿ�ʼ�˶�ʱ![]() �ٶ�v�Ĵ�С��
�ٶ�v�Ĵ�С��
��2����![]() ��ʼ�˶�����ܿ�ʼ�˶��Ĺ����У�
��ʼ�˶�����ܿ�ʼ�˶��Ĺ����У�![]() �ϲ���������
�ϲ���������![]() ����ù���
����ù���![]() λ��x�Ĵ�С��
λ��x�Ĵ�С��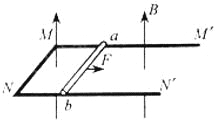
���𰸡���1��![]() 6m/s
6m/s
(2) x="1.1m "
��������
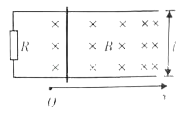
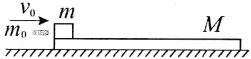
����ab�������и�Ÿ����˶���������Ӧ��������������MN��MN�ܵ����ҵİ����������������������Ħ����ʱ����ܿ�ʼ�˶������ݰ�������ŷķ���ɺ�ƽ��������֪ʶ������ٶȣ����������غ����λ�ƣ�
�⣺��1�������⣬���Ħ�������ڻ���Ħ�����������ܵ����Ħ����Ϊ��
F=��FN=����m1+m2��g
ab�еĸ�Ӧ�綯��Ϊ��E=Blv
MN�е���Ϊ��![]()
MN�ܵ��İ�����Ϊ��F��=IlB
��ܿ�ʼ�˶�ʱ�У�F��=F
��������ʽ�������ݣ���ã�v=6m/s
��2�������ab��MN�и�Ӧ����ʱ����ȣ��ɽ�������Q=I2Rt��֪��Q��R
��պϻ�·�в�������������![]() =
=![]() ��0.1J=0.4J
��0.1J=0.4J
�������غ㶨�ɣ��ã�Fx=![]() +Q��
+Q��
�������ݽ�ã�x=1.1m
�𣺣�1�����ܿ�ʼ�˶�ʱab�ٶ�v�Ĵ�СΪ6m/s��
��2����ab��ʼ�˶�����ܿ�ʼ�˶��Ĺ�����abλ��x�Ĵ�СΪ1.1m��