题目内容
8. 如图所示,质量为50kg的滑雪运动员,在倾角θ的斜坡顶端,从静止开始匀加速下滑90m到达坡底,用时10s.若g取10m/s2,求
如图所示,质量为50kg的滑雪运动员,在倾角θ的斜坡顶端,从静止开始匀加速下滑90m到达坡底,用时10s.若g取10m/s2,求(1)运动员下滑过程中的加速度大小;
(2)运动员到达坡底时的速度大小;
(3)运动员受到的合外力大小.
分析 (1)运动员沿斜坡匀加速下滑,依据运动员的运动情况,即位移、时间和初速度,由运动学位移时间公式可得加速度;
(2)由运动学速度时间公式可求得末速度.
(3)根据加速度和质量,由牛顿第二定律可求合外力大小.
解答 解:(1)根据位移时间公式,可得:x=$\frac{1}{2}$at2,
解得:a=$\frac{2x}{{t}^{2}}$=$\frac{2×90}{1{0}^{2}}$m/s2=1.8m/s2.
即运动员下滑过程中的加速度大小为1.8m/s2.
(2)根据速度时间公式可得:
v=at=1.8×10m/s=18m/s.
即运动员到达坡底时的速度大小为18m/s.
(3)根据牛顿第二定律,有:
F=ma=50×1.8N=90N
即运动员受到的合外力大小为90N.
答:(1)运动员下滑过程中的加速度大小为1.8m/s2.
(2)运动员到达坡底时的速度大小为18m/s.
(3)运动员下滑过程中所受合外力的大小为90N.
点评 本题关键根据运动学公式求解末速度和加速度,然后根据牛顿第二定律求合外力,明确动力学问题中加速度是联系运动和力的桥梁,是必求的量.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18. 物体m用线通过光滑的水平板间小孔与砝码M相连,并且正在做匀速圆周运动,如图所示,如果减少M的重量,则物体m的轨道半径r,角速度ω,线速度v的大小变化情况是( )
物体m用线通过光滑的水平板间小孔与砝码M相连,并且正在做匀速圆周运动,如图所示,如果减少M的重量,则物体m的轨道半径r,角速度ω,线速度v的大小变化情况是( )
 物体m用线通过光滑的水平板间小孔与砝码M相连,并且正在做匀速圆周运动,如图所示,如果减少M的重量,则物体m的轨道半径r,角速度ω,线速度v的大小变化情况是( )
物体m用线通过光滑的水平板间小孔与砝码M相连,并且正在做匀速圆周运动,如图所示,如果减少M的重量,则物体m的轨道半径r,角速度ω,线速度v的大小变化情况是( )| A. | r减小,v减小 | B. | r减小,v不变 | C. | r增大,ω减小 | D. | r增大,ω增大 |
16.已知物体在2N、3N、4N三个共点力的作用下处于平衡状态,若保持两个力不变撤去其中2N的力,那么其余两个力的合力大小为( )
| A. | 2 N | B. | 3N | C. | 4 N | D. | 5N |
3.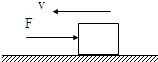 如图所示,质量m=10kg的物体在水平面上向左运动,物体与水平面间的动摩擦因数为0.2,与此同时物体受到一个水平向右的推力F=20N的作用,g取为10m/s2,则物体产生的加速度是( )
如图所示,质量m=10kg的物体在水平面上向左运动,物体与水平面间的动摩擦因数为0.2,与此同时物体受到一个水平向右的推力F=20N的作用,g取为10m/s2,则物体产生的加速度是( )
 如图所示,质量m=10kg的物体在水平面上向左运动,物体与水平面间的动摩擦因数为0.2,与此同时物体受到一个水平向右的推力F=20N的作用,g取为10m/s2,则物体产生的加速度是( )
如图所示,质量m=10kg的物体在水平面上向左运动,物体与水平面间的动摩擦因数为0.2,与此同时物体受到一个水平向右的推力F=20N的作用,g取为10m/s2,则物体产生的加速度是( )| A. | 0 | B. | 4m/s2,水平向右 | C. | 2m/s2,水平向左 | D. | 2m/s2,水平向右 |
20. 如图所示,在水平面上叠放着的两个物体A,B在水平外力F的作用下向右做匀加速运动(A,B保持相对静止),设A与B间的摩擦因数为μ1,B与地面间的动摩擦因数为μ2,则关于这两个动摩擦因数μ1,μ2的说法可能正确的是( )
如图所示,在水平面上叠放着的两个物体A,B在水平外力F的作用下向右做匀加速运动(A,B保持相对静止),设A与B间的摩擦因数为μ1,B与地面间的动摩擦因数为μ2,则关于这两个动摩擦因数μ1,μ2的说法可能正确的是( )
 如图所示,在水平面上叠放着的两个物体A,B在水平外力F的作用下向右做匀加速运动(A,B保持相对静止),设A与B间的摩擦因数为μ1,B与地面间的动摩擦因数为μ2,则关于这两个动摩擦因数μ1,μ2的说法可能正确的是( )
如图所示,在水平面上叠放着的两个物体A,B在水平外力F的作用下向右做匀加速运动(A,B保持相对静止),设A与B间的摩擦因数为μ1,B与地面间的动摩擦因数为μ2,则关于这两个动摩擦因数μ1,μ2的说法可能正确的是( )| A. | μ1=0,μ2=0 | B. | μ1=0,μ2≠0 | C. | μ1≠0,μ2=0 | D. | μ1≠0,μ2≠0 |
11. 如图所示,A、B两物体的质量比mA:mB=3:2,它们原来静止在平板车C上,A、B间有一根被压缩了的弹簧,A、B与平板车上表面间动摩擦因数相同,地面光滑.当弹簧突然释放后,则有( )
如图所示,A、B两物体的质量比mA:mB=3:2,它们原来静止在平板车C上,A、B间有一根被压缩了的弹簧,A、B与平板车上表面间动摩擦因数相同,地面光滑.当弹簧突然释放后,则有( )
 如图所示,A、B两物体的质量比mA:mB=3:2,它们原来静止在平板车C上,A、B间有一根被压缩了的弹簧,A、B与平板车上表面间动摩擦因数相同,地面光滑.当弹簧突然释放后,则有( )
如图所示,A、B两物体的质量比mA:mB=3:2,它们原来静止在平板车C上,A、B间有一根被压缩了的弹簧,A、B与平板车上表面间动摩擦因数相同,地面光滑.当弹簧突然释放后,则有( )| A. | A、B系统动量守恒 | B. | A、B、C系统不动量守恒 | ||
| C. | 小车向左运动 | D. | 小车向右运动 |
 如图所示,第四象限内有互相正交的匀强电场E与匀强磁场B1,E的大小为0.5×103V/m,B1大小为0.5T;第一象限的某个矩形区域内,有方向垂直纸面向里的匀强磁场B2,磁场的下边界与x轴重合.一质量m=1×10-14kg、电荷量q=1×10-10C的带正电微粒以某一速度v沿与y轴正方向60°角从M点沿直线运动,经P点即进入处于第一象限内的磁场B2区域.一段时间后,小球经过y轴上的N点并与y轴正方向成60°角的方向飞出.M点的坐标为(0,-10),N点的坐标为(0,30),不计粒子重力,g取10m/s2.
如图所示,第四象限内有互相正交的匀强电场E与匀强磁场B1,E的大小为0.5×103V/m,B1大小为0.5T;第一象限的某个矩形区域内,有方向垂直纸面向里的匀强磁场B2,磁场的下边界与x轴重合.一质量m=1×10-14kg、电荷量q=1×10-10C的带正电微粒以某一速度v沿与y轴正方向60°角从M点沿直线运动,经P点即进入处于第一象限内的磁场B2区域.一段时间后,小球经过y轴上的N点并与y轴正方向成60°角的方向飞出.M点的坐标为(0,-10),N点的坐标为(0,30),不计粒子重力,g取10m/s2. 现要测量某电流表的内阻,其内阻在8Ω~10Ω之间,可选用的器材如下:
现要测量某电流表的内阻,其内阻在8Ω~10Ω之间,可选用的器材如下: