Question

【题目】有两个用一根轻质弹簧相连的木块A、B静止在光滑水平面上，其质量mA=1kg、mB=2.95kg，一颗质量m=50g的子弹沿水平方向以v0=400m/s的速度，在极短时间内射穿A并留在B中，射穿A木块后子弹的速度变为原来的0.6倍。求：

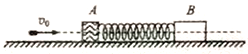
(1)子弹穿过木块A时A木块的速度vA；

(2)系统运动过程中弹簧的最大弹性势能EP；

(3)弹簧再次恢复原长时木块A、B的速度大小。

Answer 1

【答案】(1) (2) (3)

【解析】

根据题中“一根轻质弹簧相连的木块A、B静止在光滑水平面上”“在极短时间内射穿A并留在B中”可知，本题考查碰撞问题。根据碰撞问题的规律，应用动量守恒定律、机械能守恒定律等知识列式计算。

(1)子弹穿过A时，子弹与A动量守恒，设A的速度为，子弹的速度为，由动量守恒定律有：，又

解得：

(2)子弹射入并留在B内，子弹与B动量守恒，设子弹与B共同的速度为，由动量守恒定律：

解得：

子弹、A、B和弹簧所组成的系统动量守恒，弹簧弹性势能最大时A、B、子弹具有相同的速度

由动量守恒定律：

解得：

由能量关系：

解得：

(3)从子弹射入B中到弹簧再次恢复原长，系统总动量守恒，总动能不变，则：

解得：或 或

弹簧再次恢复原长时木块A、B的速度大小分别为