题目内容
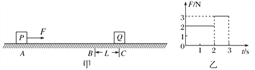
【题目】如图甲所示,质量均为m=0.5 kg的相同物块P和Q(可视为质点)分别静止在水平地面上A、C两点.P在按图乙所示随时间变化的水平力F作用下由静止开始向右运动,3 s末撤去力F,此时P运动到B点,之后继续滑行并与Q发生弹性碰撞.已知B、C两点间的距离L=3.75 m,P、Q与地面间的动摩擦因数均为μ=0.2,取g=10 m/s2,求:
(1)P到达B点时的速度大小v及其与Q碰撞前瞬间的速度大小v1;
(2)Q运动的时间t.
【答案】(1)![]() ,
, ![]() (2)
(2)![]()
【解析】(1)在0-3s内,对P,由动量定理有:
F1t1+F2t2-μmg(t1+t2)=mv-0
其中F1=2N,F2=3N,t1=2s,t2=1s
解得:v=8m/s
设P在BC两点间滑行的加速度大小为a,由牛顿第二定律可得:μmg=ma
P在BC两点间做匀减速直线运动,有:v2-v12=2aL
解得:v1=7m/s
(2)设P与Q发生弹性碰撞后瞬间的速度大小分别为v1′、v2′,取向右为正方向,由动量守恒定律和动能守恒有:
mv1=mv1′+mv2′![]() mv12=
mv12=![]() mv1′2+
mv1′2+![]() mv2′2
mv2′2
联立解得:v2′=v1=7m/s
碰后Q做匀减速直线运动,加速度为:a′=μg=2m/s2
Q运动的时间为:![]()

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目




