题目内容
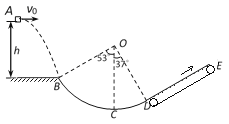
【题目】如图所示倾角为370的斜面上，有一质量为1.5千克的木板A，在木板A的顶端放有质量为4.5千克的木块B，木板A右端距离斜面末端1m处的D处有一物C,木板A与斜面间的动摩擦因数为μ1=0.2,木块B与木板A之间的动摩擦因数为μ2=0.1。斜面的末端D处有一半径r=0.125米的光滑圆弧轨道，与斜面相切于D点，轨道的末端为最高点E。某时刻起,从静止开始释放木块B与木板A，木板A与物块C发生弹性碰撞后,木板被弹回。（此时木块B扔在木板A上），而物块C最终从圆弧轨道滑下回到碰撞点，重力加速度g=10m/s2求：
（1）物块C的质量的取值范围
（2）若木板的反弹速度为1.48m/s，且木块B滑离木板时，木板速度恰好为零，（此时木板仍在斜面上），试确定物块C离开圆弧形轨道的位置及木板的长度。
【答案】（1）
（2）物块C从D点离开圆弧轨道；2.22m.
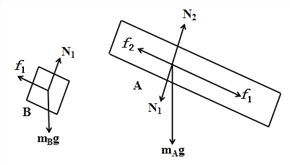
【解析】（1）对A、B受力分析如图所示，由木块B受力分析得：
解得aB=5.2m/s2
由木板A受力分析得：
解得 aA=2m/s
木板A到达D处过程中，由运动学公式有2aAL=v12
解得木板A到达D处时的速度v1=2m/s
木板A与物块C发生弹性碰撞，由动量守恒定律有：
由机械能守恒有
联立解得：碰撞后木板A的速度
，碰撞后物块C的速度
由于木板A被弹回，可知
的方向与v1相反，mA<mC，即mC>1.5kg
由于物块C可以从圆弧轨道滑下来，设物块C在D处获得的最大速度为vCm
由动能定理得
解得：vCm=
m/s
故vC<vCm，代入上式，解得
综上：
木板A运动到D处所用的时间为
这个过程中木板B的位移为
此时vB=aBt1=5.2m/s
碰后木块B的加速度不变，木板A的加速度满足：
解得
木板A减速到0所用的时间
板长
，故物块C从D点离开圆弧轨道。
