题目内容
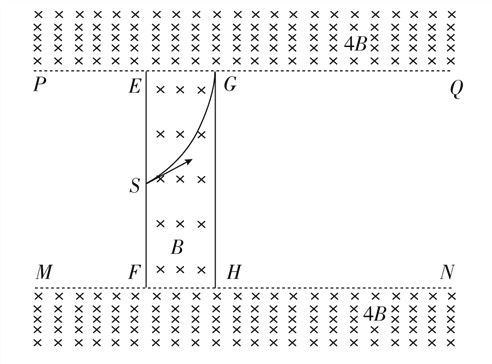
【题目】如图所示,边界PQ以上和MN以下空间存在垂直纸面向里的匀强磁场,磁感应强度均为4B,PQ、MN间距离为2![]() d,绝缘板EF、GH厚度不计,间距为d,板长略小于PQ、MN间距离,EF、GH之间有垂直纸面向里的匀强磁场,磁感应强度为B。有一个质量为m的带正电的粒子,电量为q,从EF的中点S射出,速度与水平方向成30°角,直接到达PQ边界并垂直于边界射入上部场区,轨迹如图所示,以后的运动过程中与绝缘板相碰时无能量损失且遵循反射定律,经过一段时间后该粒子能再回到S点。(粒子重力不计) 求:
d,绝缘板EF、GH厚度不计,间距为d,板长略小于PQ、MN间距离,EF、GH之间有垂直纸面向里的匀强磁场,磁感应强度为B。有一个质量为m的带正电的粒子,电量为q,从EF的中点S射出,速度与水平方向成30°角,直接到达PQ边界并垂直于边界射入上部场区,轨迹如图所示,以后的运动过程中与绝缘板相碰时无能量损失且遵循反射定律,经过一段时间后该粒子能再回到S点。(粒子重力不计) 求:
(1)粒子从S点出发的初速度v;
(2)粒子从S点出发第一次再回到S点的时间;
(3)若其他条件均不变,EF板不动,将GH板从原位置起向右平移,且保证EFGH区域内始终存在垂直纸面向里的匀强磁场B,若仍需让粒子回到S点(回到S点的运动过程中与板只碰撞一次),则GH到EF的垂直距离x应满足什么关系?(用d来表示x)
【答案】(1)v=![]() (2)
(2)![]() (3)x=(3n+1)d,(n=0,1,2…)或x=3nd,(n=0,1,2…)。
(3)x=(3n+1)d,(n=0,1,2…)或x=3nd,(n=0,1,2…)。
【解析】试题分析:(1)![]() ,且s为中点,
,且s为中点,![]() ,
,![]()
![]() ,
,![]() ,
,
![]()
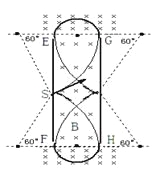
(2) 如图,粒子应从G点进入PQ的磁场,
在4B场内,![]() ,
,![]()
做半圆,并垂直PQ再由E点回到B场区
由对称性,粒子将打到GH中点并反弹,再次回到S点的轨迹如上图
粒子在B场中时间![]()
粒子在4B场中时间![]()

![]()
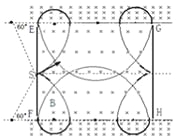
(3)如图所示,由粒子运行的周期性以及与板碰撞遵循反射定律,有如下结果:
![]() 或
或![]()

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目