题目内容
【题目】物理学中,力与运动关系密切,而力的空间积累效果——做功,又是能量转化的量度。因此我们研究某些运动时,可以先分析研究对象的受力特点,进而分析其能量问题。已知重力加速度为![]() ,且在下列情境中,均不计空气阻力。
,且在下列情境中,均不计空气阻力。
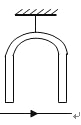
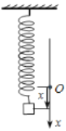
(1)劲度系数为![]() 的轻质弹簧上端固定,下端连一可视为质点的小物块,若以小物块的平衡位置为坐标原点
的轻质弹簧上端固定,下端连一可视为质点的小物块,若以小物块的平衡位置为坐标原点![]() ,以竖直向下为正方向建立坐标轴
,以竖直向下为正方向建立坐标轴![]() ,如图所示,用
,如图所示,用![]() 表示小物块由平衡位置向下发生的位移。求小物块的合力
表示小物块由平衡位置向下发生的位移。求小物块的合力![]() 与
与![]() 的关系式,并据此说明小物块的运动是否为简谐运动;
的关系式,并据此说明小物块的运动是否为简谐运动;
(2)系统的总势能为重力势能与弹性势能之和。请你结合小物块的受力特点和求解变力功的基本方法,以平衡位置为系统总势能的零势能参考点,推到小物块振动位移为![]() 时系统总势能
时系统总势能![]() 的表达式。
的表达式。
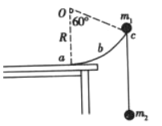
(3)如图所示为理想单摆,摆角![]() 最够小,可认为是简写运动。其平衡位置记为
最够小,可认为是简写运动。其平衡位置记为![]() 点。若已知摆球的质量为
点。若已知摆球的质量为![]() ,摆长为
,摆长为![]() ,在偏角很小时,摆球对于
,在偏角很小时,摆球对于![]() 点的位移
点的位移![]() 的大小与
的大小与![]() 角对应的弧长、弦长都近似相等,即近似满足:
角对应的弧长、弦长都近似相等,即近似满足:![]() 。请推导得出小球在任意位置处的回复力与位移的比例常数
。请推导得出小球在任意位置处的回复力与位移的比例常数![]() 的表达式。
的表达式。

【答案】(1)![]() 小物块的运动是简谐运动(2)
小物块的运动是简谐运动(2)![]() (3)推导见解析,
(3)推导见解析,![]()
【解析】
(1)设小物块位于平衡位置时弹簧的伸长量为x0,有
![]()
当小物块相对于平衡位置的向下位移为x时,受弹力FT和重力G作用,如左图所示,合力
![]()
![]()
![]()
解得
![]()
即合力与位移大小成正比,方向相反,说明小物块的运动是简谐运动;
(2)合力F与位移x关系图线如图所示。由图可知物块由平衡位置到位移为x处的运动过程中合力F做的功

![]()
由动能定理有
![]()
依据机械能守恒定律有
![]()
得
![]()
以平衡位置为零势能参考点,则
![]()
(3)摆球位移为x'处,受力示意图见图所示:
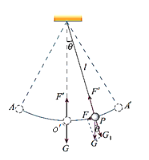
以O'为原点,以水平向右的方向为x轴的正方向建立坐标系,在摆角很小时
![]()
在摆球位移为x'时,回复力为
![]()
比例常数为
![]()

练习册系列答案
相关题目