Question

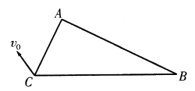
【题目】如图所示，圆心在O点、半径为R的圆弧轨道abc竖直固定在水平桌面上，Oc与Oa的夹角为60°，轨道最低点a与桌面相切．一轻绳两端分别系着质量为m1和m2的小球（均可视为质点），挂在圆弧轨道边缘c的两边，开始时，m1在c点从静止释放．设轻绳足够长，不计一切摩擦．则( 　)

A.在m1下滑过程中，两球速度大小始终相等

B.m1在由c下滑到a的过程中重力的功率逐渐增大

C.若m1恰好能沿圆弧下滑到a点，则m1=2m2

D.若m1=4m2，则m1下滑到a点速度大小为

Answer 1

【答案】CD

【解析】

A．m1由C点下滑到a点的过程中，沿绳子方向的速度是一样的，在m1滑下去一段过程以后，此时的绳子与圆的切线是不重合，而是类似于圆的一根弦线而存在，所以此时两个物体的速度必然不相同的，故A错误；
B．重力的功率就是P=mgv，这里的v是指竖直的分速度，一开始m1是由静止释放的，所以m1一开始的竖直速度也必然为零，最后运动到A点的时候，由于此时的切线是水平的，所以此时的竖直速度也是零，但是在这个c到a的过程当中是肯定有竖直分速度的，所以相当于竖直速度是从无到有再到无的一个过程，也就是一个先变大后变小的过程，所以这里重力功率mgv也是先增大后减小的过程，故B错误；
C．若m1恰好能沿圆弧轨道下滑到a点，此时两小球速度均为零，根据动能定理得：

m1gR（1-cos60°）=m2gR，

解得：

m1=2m2

选项C正确；
D．若m1=4m2，设m1下滑到a点速度大小为v，则

解得

故D正确。
故选CD。