��Ŀ����
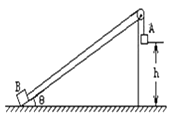
����Ŀ����ͼ��ʾ��һ�㹻���Ĺ̶�б����Ǧ�=37�㣬�����A��B�������ֱ�ΪmA��mB�ֱ�Ϊ1kg��4kg��������б��֮��Ķ�Ħ��������Ϊ��=0.5�������֮���������L=0.5m���������ܵ��������T=12N��������B����б�����ϵ���F������ʹA��Bһ���ɾ�ֹ��ʼ��б�������˶���gȡ10m/s2 �� ��sin37��=0.6��cos37��=0.8��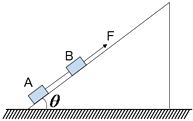
��1��ijһʱ�����������ϣ����ʱ����F�Ĵ�С��
��2������������ǰ˲��A��B���ٶ�Ϊ3m/s�����Ϻ�����F���䣬��A�˶�����ߵ�ʱ��A��B֮��ľ��룮
���𰸡�
��1��
�⣺���������������ţ�ٵڶ����ɵã�
F����mA+mB��gsin�ȩ��̣�mA+mB��gcos��=mA+mB��a��
A���壺T��mAgsin�ȩ���mAgcos��=mAa��
�������ݽ�ã�a=2m/s2��F=60N��
��2��
�⣺����б������Ϊ����A���壺
��mAgsin�ȩ���mAgcos��=mAaA����ã�aA=��10m/s2��
��Ϊv0=3m/s������A���嵽��ߵ�Ϊ��t= ![]() =
= ![]() =0.3s��
=0.3s��
�˹���A�����λ��Ϊ��xA= ![]() t=0.45m��
t=0.45m��
��B���壺F��mBgsin�ȩ���mBgcos��=mBaB��
�������ݽ�ã�aB=5m/s2��
B��λ�ƣ�xB=v0t+ ![]() aBt2=1.125m��
aBt2=1.125m��
�������������x=xB��xA+L
�������ݽ�ã���x=1.175m
����������1�����������������ţ�ٵڶ������������ļ��ٶȣ��ٸ����A����������ţ�ٵڶ������������F�Ĵ�С����2������ţ�ٵڶ�����������Ϻ�A��B�ļ��ٶȣ�����ٶ�ʱ�乫ʽ���A�ٶȼ�Ϊ���ʱ�䣬�Ӷ�������ʱ����A��B��λ�ƣ�����λ�ƹ�ϵ���A��B��ľ��룮