题目内容
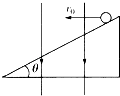
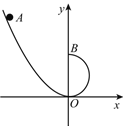
【题目】如图所示，在竖直平面内有一直角坐标系
，在坐标系的第二象限内有一粗糙曲面轨道，在第一象限内有一半径为
的光滑半圆弧轨道（圆心在
轴上），它们恰好在
点平滑连接．现让一质量为
的小球（可视为质点）从左侧距
轴竖直高度为
的
点由静止释放，到达
点时的速度大小是
，已知重力加速度为
．求：
（
）小球由
到
克服摩擦力做的功；
（
）小球到最高点
时对轨道的压力；
（
）若所有轨道均光滑，且左侧轨道满足的方程为
，要使小球能过圆弧轨道的最高点
，求小球从左侧轨道由静止释放的最低位置坐标．
【答案】（
）mgR；（
）mg，方向向上；（
）
．
【解析】（
）小球由
到
，由动能定理得： 
据题
解得，小球克服摩擦力做的功
（
）小球由
到
，由动能定理得： 
在
点，由合力提供向心力，由牛顿第二定律得： 
联立解得
由牛顿第三定律知，小球在
点对轨道的压力大小为
，方向向上．
（
）规定
思所在平面势能为零，设释放的最低位置坐标为
， 
点的最小速度为
．
对全过程，运用机械能守恒定律得： 
在
点，有
联立得
将
代入抛物线方程
，得
所以，最低位置坐标为
．
练习册系列答案
相关题目
