Question

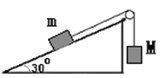
【题目】如图所示，质量都是m的物体A和B，通过轻绳子跨过滑轮相连．斜面光滑，不计绳子和滑轮之间的摩擦．开始时A物体离地的高度为h，B物体位于斜面的底端，用手托住A物体，A、B两物均静止．撤去手后，求：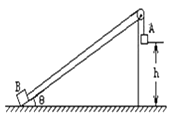

（1）A物体将要落地时的速度多大？
（2）A物落地后，B物由于惯性将继续沿斜面上升，则B物在斜面上的最远点离地的高度多大？

Answer 1

【答案】
（1）解：A、B两物构成的整体（系统）只有重力做功，故整体的机械能守恒，得：

mgh﹣mghsinθ= （m+m）v2

整理得v=

（2）解：当A物体落地后，B物体由于惯性将继续上升，此时绳子松了，对B物体而言，只有重力做功，故B物体的机械能守恒，设其上升的最远点离地高度为H，根据机械能守恒定律得：

mv2=﹣mg（H﹣h sinθ）

整理得H= h（1+sinθ）．

【解析】选两物体作为整体来研究时机械能守恒，从而求出A物体下落的速度．当物体A落地后，物体B由于惯性继续上升，由机械能守恒定律可求出B物在斜面上的最远点离地的高度．
【考点精析】通过灵活运用机械能守恒及其条件，掌握在只有重力（和弹簧弹力）做功的情形下，物体动能和重力势能（及弹性势能）发生相互转化，但机械能的总量保持不变即可以解答此题．