题目内容
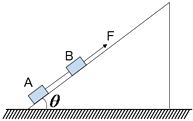
【题目】如图所示，传送带与水平面之间的夹角θ=30°，其上A、B两点间的距离L=5m，传送带在电动机的带动下以v=1m/s的速度匀速运动．现将一质量m=10kg 的小物体（可视为质点）轻放在传送带的A点，已知小物体与传送之间的动摩擦因数μ= 
，在传送带将小物体从A点传送到B点的过程中，求：（取g=10m/s2）
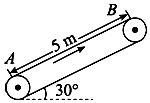
（1）物体刚开始运动的加速度大小；
（2）物体从A到B运动的时间
（3）传送带对小物体做的功；
（4）电动机做的功．
【答案】
（1）解：小物体加速过程，根据牛顿第二定律有：
μmgcos θ﹣mgsin θ=ma
则得物体上升的加速度为：a= 
g=2.5 m/s2
答：物体刚开始运动的加速度大小是2.5 m/s2；
（2）解：当小物体的速度增加到 v=1 m/s时，通过的位移是：x1= 
= 
m=0.2 m
由v=at得：t1= 
= 
s=0.4 s
由于μmgcos θ＞mgsin θ，所以物体与传送带同速一起匀速运动，位移为 x2=L﹣x1=5m﹣0.2m=4.8m，即小物体将以v=1 m/s的速度完成4.8 m的路程
用时为：t2= 
= 
s=4.8s
故总时间为：t=t1+t2=5.2s
答：物体从A到B运动的时间是5.2s；
（3）解：由功能关系得：传送带对小物体做的功为：W=△Ep+△Ek=mgLsin θ+ 
mv2
代入数据解得：W=255 J．
答：传送带对小物体做的功是255 J；
（4）解：电动机做功使小物体机械能增加，同时小物体与传送带间因摩擦产生热量Q，相对位移为：x′=vt1﹣ vt1= vt1= 
m=0.2 m
摩擦生热为：Q=μmgx′cos θ= 
×10×10×0.2× =15 J
故电动机做的功为：W电=W+Q=270 J．
答：电动机做的功是270 J．
【解析】（1）对物体进行受力分析，根据牛顿第二定律求出小物体刚开始运动的加速度．（2）物体运动的总时间为匀加速运动与匀速运动的时间之和；根据运动学公式求解时间．（2）由功能关系知，传送带对小物体做的功等于小物体机械能的增量．（3）电动机多做的功等于小物体机械能的增量和系统摩擦产生的内能之和．
