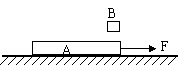题目内容
一质量为2Kg木块放在水平面上,木块与水平面的动摩擦因数u=0.5,现在斜向上的拉力F作用下从静止开始做匀加速直线运动,10秒后撤去拉力F,木块便减速到最后静止.已知F=10N,与水平面夹角α=37°,重力加速度g=10m/s2.求木块总位移和总时间为多少?
设木块匀加速直线运动和匀减速直线运动的加速度大小分别为a1和a2.
根据牛顿第二定律得:
a1=
=
m/s2=0.5m/s2
a2=
=μg=5m/s2
10秒后撤去拉力F时木块的速度为v=a1t1=5m/s.设木块匀减速运动的时间为t2.则:
t2=
=1s
所以木块运动的总时间为:t=t1+t2=11s
匀加速运动的位移为:x1=
a1
=
×0.5×102m=25m
匀减速运动的位移为:x2=
=
m=2.5m
所以木块的总位移为x=x1+x2=27.5m
答:木块的总位移为27.5m,总时间为11s.
根据牛顿第二定律得:
a1=
| Fcos37°-μ(mg-Fsin37°) |
| m |
| 10×0.8-0.5(20-10×0.6) |
| 2 |
a2=
| μmg |
| m |
10秒后撤去拉力F时木块的速度为v=a1t1=5m/s.设木块匀减速运动的时间为t2.则:
t2=
| v |
| a2 |
所以木块运动的总时间为:t=t1+t2=11s
匀加速运动的位移为:x1=
| 1 |
| 2 |
| t | 21 |
| 1 |
| 2 |
匀减速运动的位移为:x2=
| vt2 |
| 2 |
| 5×1 |
| 2 |
所以木块的总位移为x=x1+x2=27.5m
答:木块的总位移为27.5m,总时间为11s.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
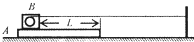 水平桌面上放着质量m1=2kg 的木板A,木板A 上放着一个装有小马达的滑块B,滑块和马达的总质量m2=1kg 一根细线一端拴在固定于桌面的小柱子上,另一端与小马达相连,如图所示,开始时,用手抓住木板A 使它不动,开启小马达,小马达转动时可以使细线卷在轴筒上,从而使滑块B 以v0=0.4m/s 的恒定速度在术板A上滑动.当滑块B与木板A 右端相距L=1m 时立即放开木板A.已知木板A 与滑块B、木板A 与地面之间动摩擦因数分别为μ1=0.05和μ2=0.01.设最大静摩力等于滑动摩擦力.(取g=10m/s2)
水平桌面上放着质量m1=2kg 的木板A,木板A 上放着一个装有小马达的滑块B,滑块和马达的总质量m2=1kg 一根细线一端拴在固定于桌面的小柱子上,另一端与小马达相连,如图所示,开始时,用手抓住木板A 使它不动,开启小马达,小马达转动时可以使细线卷在轴筒上,从而使滑块B 以v0=0.4m/s 的恒定速度在术板A上滑动.当滑块B与木板A 右端相距L=1m 时立即放开木板A.已知木板A 与滑块B、木板A 与地面之间动摩擦因数分别为μ1=0.05和μ2=0.01.设最大静摩力等于滑动摩擦力.(取g=10m/s2)