题目内容
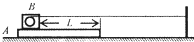 水平桌面上放着质量m1=2kg 的木板A,木板A 上放着一个装有小马达的滑块B,滑块和马达的总质量m2=1kg 一根细线一端拴在固定于桌面的小柱子上,另一端与小马达相连,如图所示,开始时,用手抓住木板A 使它不动,开启小马达,小马达转动时可以使细线卷在轴筒上,从而使滑块B 以v0=0.4m/s 的恒定速度在术板A上滑动.当滑块B与木板A 右端相距L=1m 时立即放开木板A.已知木板A 与滑块B、木板A 与地面之间动摩擦因数分别为μ1=0.05和μ2=0.01.设最大静摩力等于滑动摩擦力.(取g=10m/s2)
水平桌面上放着质量m1=2kg 的木板A,木板A 上放着一个装有小马达的滑块B,滑块和马达的总质量m2=1kg 一根细线一端拴在固定于桌面的小柱子上,另一端与小马达相连,如图所示,开始时,用手抓住木板A 使它不动,开启小马达,小马达转动时可以使细线卷在轴筒上,从而使滑块B 以v0=0.4m/s 的恒定速度在术板A上滑动.当滑块B与木板A 右端相距L=1m 时立即放开木板A.已知木板A 与滑块B、木板A 与地面之间动摩擦因数分别为μ1=0.05和μ2=0.01.设最大静摩力等于滑动摩擦力.(取g=10m/s2)(1)通过计算判断松手后木板A 是否会在桌面上滑动?
(2)求松手后滑块B 与木块A相互摩擦而产生的内能E.
分析:(1)分别求出A、B之间的滑动摩擦力大小以及桌面对A的最大静摩擦力大小,通过比较两个摩擦力的大小关系,判断木板是否在桌面上滑动.
(2)根据牛顿第二定律求出木板的加速度,当A、B速度相同后,保持相对静止一起做匀速直线运动,结合运动学公式求出两者的相对位移大小,从而得出摩擦产生的内能.
(2)根据牛顿第二定律求出木板的加速度,当A、B速度相同后,保持相对静止一起做匀速直线运动,结合运动学公式求出两者的相对位移大小,从而得出摩擦产生的内能.
解答:解:(1)滑块B对木板A的滑动摩擦力为:
FBA=μ1m2g
得:FBA=0.5N
桌面对木板A的最大静摩擦力为:
Fmax=μ2(m1+m2)g
得:Fmax=0.3N
因Fmax<FBA,故木板A会在桌面上滑动.
(2)设桌面对A的滑动摩擦力为FA,有:
FA=μ2(m1+m2)g
设木板A的加速度为a,由牛顿第二定律,有:
FBA-FA=m1a
得:a=
=
=0.1m/s2
设经过时间t,A的速度达到v0,则有:
v0=at
解得:t=
=
s=4s
时间t内A、B的位移分别为:
SA=
at2=
×0.1×16m=0.8m,SB=v0t=0.4×4m=1.6m
所以有:SB-SA=0.8m<L,B不会从A上滑落,
由功能关系可得:E=FBA(SB-SA)
综合以上各式,可得:E=0.4J.
答:(1)木板A会在桌面上滑动.
(2)松手后滑块B 与木块A相互摩擦而产生的内能为0.4J.
FBA=μ1m2g
得:FBA=0.5N
桌面对木板A的最大静摩擦力为:
Fmax=μ2(m1+m2)g
得:Fmax=0.3N
因Fmax<FBA,故木板A会在桌面上滑动.
(2)设桌面对A的滑动摩擦力为FA,有:
FA=μ2(m1+m2)g
设木板A的加速度为a,由牛顿第二定律,有:
FBA-FA=m1a
得:a=
| FBA-FA |
| m1 |
| 0.5-0.3 |
| 2 |
设经过时间t,A的速度达到v0,则有:
v0=at
解得:t=
| v0 |
| a |
| 0.4 |
| 0.1 |
时间t内A、B的位移分别为:
SA=
| 1 |
| 2 |
| 1 |
| 2 |
所以有:SB-SA=0.8m<L,B不会从A上滑落,
由功能关系可得:E=FBA(SB-SA)
综合以上各式,可得:E=0.4J.
答:(1)木板A会在桌面上滑动.
(2)松手后滑块B 与木块A相互摩擦而产生的内能为0.4J.
点评:本题综合考查了牛顿第二定律和运动学公式的运用,关键是理清木板和滑块的运动情况,结合牛顿第二定律和运动学公式进行求解.

练习册系列答案
相关题目
 如图所示,在水平桌面上叠放着质量相等的A、B两块木板,在木板A上放着一个物块C,木板和物块均处于静止状态.已知物块C的质量为m,A、B、C之间以及B与地面之间的动摩擦因数均为μ.用水平恒力F向右拉动木板A使之做匀加速运动,物块C始终与木板A保持相对静止.设最大静摩擦力与滑动摩擦力大小相等,重力加速度为g.则以下判断正确的是( )
如图所示,在水平桌面上叠放着质量相等的A、B两块木板,在木板A上放着一个物块C,木板和物块均处于静止状态.已知物块C的质量为m,A、B、C之间以及B与地面之间的动摩擦因数均为μ.用水平恒力F向右拉动木板A使之做匀加速运动,物块C始终与木板A保持相对静止.设最大静摩擦力与滑动摩擦力大小相等,重力加速度为g.则以下判断正确的是( )