题目内容
(18分)如图所示,半径为 的 1/4光滑圆弧轨道最低点D与水平面相切,在D点右侧
的 1/4光滑圆弧轨道最低点D与水平面相切,在D点右侧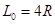 处用长为
处用长为 的细绳将质量为
的细绳将质量为 的小球B(可视为质点)悬挂于O点,小球B的下端恰好与水平面接触,质量为
的小球B(可视为质点)悬挂于O点,小球B的下端恰好与水平面接触,质量为 的小球A(可视为质点)自圆弧轨道C的正上方H高处由静止释放,恰好从圆弧轨道的C点切入圆弧轨道,已知小球A与水平面间的动摩擦因数
的小球A(可视为质点)自圆弧轨道C的正上方H高处由静止释放,恰好从圆弧轨道的C点切入圆弧轨道,已知小球A与水平面间的动摩擦因数 ,细绳的最大张力
,细绳的最大张力 ,重力加速度为
,重力加速度为 ,试求:
,试求: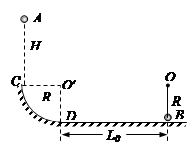
(1)若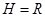 ,小球A到达圆弧轨道最低点D时所受轨道的支持力;
,小球A到达圆弧轨道最低点D时所受轨道的支持力;
(2)试讨论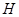 在什么范围内,小球A与B发生弹性碰撞后细绳始终处于拉直状态。
在什么范围内,小球A与B发生弹性碰撞后细绳始终处于拉直状态。
(1)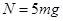 ,方向竖直向上。(2)
,方向竖直向上。(2)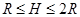 和
和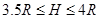
解析试题分析: (1)设小球运动到D点的速度为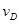
对小球在从静止上落到D点时,由机械能守恒定律: ①
①
在D点由牛顿第二定律: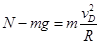 ②
②
由①②得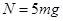 ,方向竖直向上。
,方向竖直向上。
(2)设A与B碰前速度为 ,碰后A的速度为
,碰后A的速度为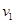 ,B的速度为
,B的速度为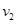 ,
,
则A与B碰撞过程有: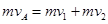 ③
③
弹性碰撞满足机械能守恒: ④
④
由③④得A、B在碰撞过程中会发生速度交换。 ,
,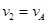 ⑤
⑤
A在由静止到碰撞前过程由动能定理有: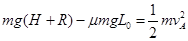 ⑥
⑥
若碰后B能在竖直平面内做完整的圆周运动,则细绳始终处于拉直状态,设小球B在最高处速度为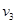 ,
,
则在最高处有: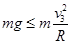 ,得
,得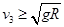 ⑦
⑦
小球B在最低点时细绳受力最大,则有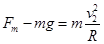 ⑧
⑧
小球B从最低点到最高点由动能定理有: ⑨
⑨
联立①④⑤⑥⑦⑧⑨解得: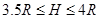 ⑩
⑩
若A与B碰后B摆动的最大高度小于 ,则细绳也始终处于拉直状态,
,则细绳也始终处于拉直状态,
则根据机械能守恒有: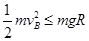 ?
?
要保证A与B能发生碰撞,则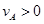 ?
?
联立①④⑤⑥??解得: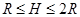 ?
?
故小球A与B发生弹性碰撞后细绳始终处于拉直状态的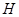 范围:
范围: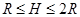 和
和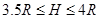
考点:本题考查了动量守恒定律、能量守恒定律、动能定理、牛顿第二定律。

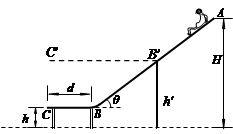
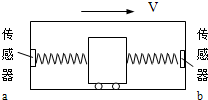
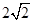 m,质量M= 3kg,滑块质量m=2kg,滑块与木板、木板与地面间的动摩擦因数均为
m,质量M= 3kg,滑块质量m=2kg,滑块与木板、木板与地面间的动摩擦因数均为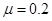 (取g=10
(取g=10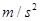 ,设最大静摩擦力等于滑动摩擦力),求:
,设最大静摩擦力等于滑动摩擦力),求:
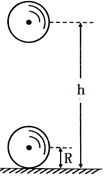
 =0.80m的轻绳一端固定在
=0.80m的轻绳一端固定在 点,另一端连接一质量
点,另一端连接一质量 距离水平地面的高度H = 1.00m。开始时小球处于
距离水平地面的高度H = 1.00m。开始时小球处于 点,此时轻绳拉直处于水平方向上,如图所示。让小球从静止释放,当小球运动到
点,此时轻绳拉直处于水平方向上,如图所示。让小球从静止释放,当小球运动到 正下方一个固定的钉子P时立刻断裂。不计轻绳断裂的能量损失,取重力加速度g=10m/s2。求:
正下方一个固定的钉子P时立刻断裂。不计轻绳断裂的能量损失,取重力加速度g=10m/s2。求: 
 点时的速度大小;
点时的速度大小; 点抛出并落在水平地面的C点,求C点与
点抛出并落在水平地面的C点,求C点与 点之间的水平距离;
点之间的水平距离;
