题目内容
（14分）如图所示，左右两端的AM、NB为竖直平面内的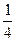
光滑圆弧轨道，半径均为
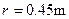，质量
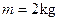的物体从左端最高点A由静止下滑，经过一段长度为
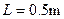粗糙的水平轨道MN后，冲上右端的光滑圆弧轨道．物体与粗糙的水平轨道间的动摩擦因数
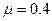，取当地的重力加速度
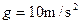，试求：
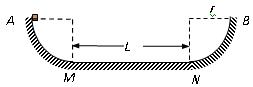
（1）物体到达右端圆弧轨道的最大高度；
（2）物体第一次经过M点（圆弧轨道的最低点）时受到轨道支持力的大小；
（3）物体第二次经过M点时速度的大小．
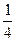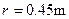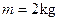光滑圆弧轨道，半径均为，质量的物体从左端最高点A由静止下滑，经过一段长度为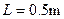粗糙的水平轨道MN后，冲上右端的光滑圆弧轨道．物体与粗糙的水平轨道间的动摩擦因数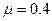，取当地的重力加速度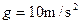，试求：（1）物体到达右端圆弧轨道的最大高度；
（2）物体第一次经过M点（圆弧轨道的最低点）时受到轨道支持力的大小；
（3）物体第二次经过M点时速度的大小．
（1）
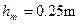
（2）
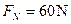
（3）
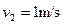
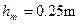
（2）
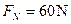
（3）
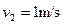
解：（1）设物体到达右端圆弧轨道的最大高度为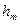
，根据动能定理得
-----------------------------------------------3分
解得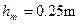：------------------------------------------------------1分
（2）设物体第一次经过M点时的速度大小为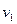
，受到轨道支持力的大小为
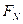．由于物体由A点运动到M点，只有重力做功，所以物体的机械能守恒．
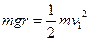---------------------------------------------------------3分
根据牛顿第二定律有：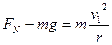
----------------------------------------------------2分
联立解得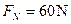-----------------------------------------------------1分
（3）设物体第二次经过M点时的速度大小为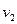
，根据动能定理有
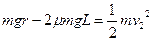------------------------------------------------3分
解得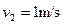：-------------------------------------------------------1分
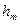，根据动能定理得-----------------------------------------------3分解得：
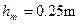------------------------------------------------------1分（2）设物体第一次经过M点时的速度大小为
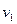，受到轨道支持力的大小为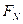．由于物体由A点运动到M点，只有重力做功，所以物体的机械能守恒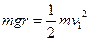．---------------------------------------------------------3分根据牛顿第二定律有：
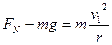----------------------------------------------------2分联立解得
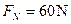-----------------------------------------------------1分（3）设物体第二次经过M点时的速度大小为
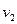，根据动能定理有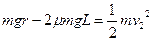------------------------------------------------3分解得：
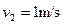-------------------------------------------------------1分
练习册系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
激活思维优加课堂系列答案
相关题目
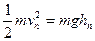?_________,理由是________________________,列出点n处瞬时速度的计算式vn=________cm/s.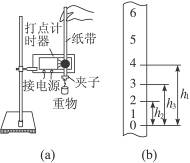
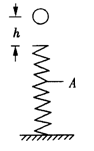
，小球2静止在最低点B，小球1从距地面某一高度沿斜轨道静止下滑，且于B位置与2相撞，球1和球2的对心碰撞时间极短且无机构能损失，碰后球1和球2的动量大小之比为1：2，方向相同，球2恰能到达C点，不计摩擦及空气阻力，重力加速度为g，求：
链条全部滑离桌面时速度为多少.