题目内容
一物体放在倾角为θ的斜面上，它刚好能沿斜面匀速下滑．
（1）求物体沿斜面下滑的动摩擦因数；
（2）若给它一个沿斜面向上的初速度v0，则它能上滑的最大距离是多少？（已知重力加速度为g，斜面始终是静止的）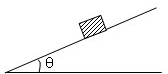
（1）求物体沿斜面下滑的动摩擦因数；
（2）若给它一个沿斜面向上的初速度v0，则它能上滑的最大距离是多少？（已知重力加速度为g，斜面始终是静止的）
（1）根据共点力平衡得，
N=mgcosθ，f=mgsinθ
由f=μN得，μ=
=
=tanθ
故物体沿斜面下滑的动摩擦因数为tanθ．
（2）物体沿斜面上滑的合力F合=mgsinθ+μmgcosθ
根据牛顿第二定律得，a=
=gsinθ+μgcosθ=2gsinθ
所以上滑的最大距离x=
=
．
故能上滑的最大距离是
．
N=mgcosθ，f=mgsinθ
由f=μN得，μ=
| f |
| N |
| mgsinθ |
| mgcosθ |
故物体沿斜面下滑的动摩擦因数为tanθ．
（2）物体沿斜面上滑的合力F合=mgsinθ+μmgcosθ
根据牛顿第二定律得，a=
| F合 |
| m |
所以上滑的最大距离x=
| 0-v02 |
| 2a |
| v02 |
| 4gsinθ |
故能上滑的最大距离是
| v02 |
| 4gsinθ |
练习册系列答案
相关题目
一物体放在倾角为θ的斜面上，它刚好能沿斜面匀速下滑．
