题目内容
（13分）一质量m=1kg的物体放在倾角θ为37°的斜面上，受到F=32N的水平推力作用从静止开始沿斜面向上运动。物体与斜面之间的动摩擦因数μ=0.5。推力F作用3s后撤去推力。求物体再运动3s后距出发点的距离。设斜面足够长，g=10m/s2
【答案】
41.76m
【解析】物体受力如图1，建坐标系得：
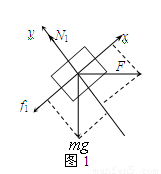
Fcosθ-mgsinθ-f1=ma1 ①
N1=Fsinθ+mgcosθ ②
f1=μN1 ③
解之a1=6m/s2 ④
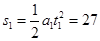m
⑤
v1=a1t1=18m/s ⑥
去掉F，物体受力如图2所示
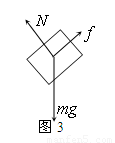
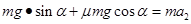⑦
解之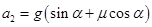
=10m/s2⑧
设经过t2时间物体速度减为零
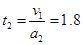s⑨
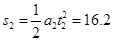m⑩
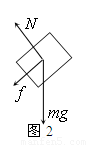
物体速度减为零后，由于μ<tanθ故物体会下滑，加速度
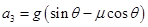
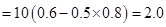m/s2
⑾
下滑位移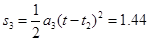
m （12）
物体距出发点的距离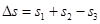 
=41.76m （13）
本题考查对牛顿第二定律的应用，以物体为研究对象进行受力分析，建立直角坐标系，把力分解后列牛顿第二定律公式，可求得加速度大小，再由运动学公式求解
练习册系列答案
相关题目
如图所示，AB、CD为光滑水平轨道，DE是半径为R1=0.3m的
（2011?洪山区模拟）如图所示，在光滑的水平面上，有一质量M=3kg的薄板和一质量m=1kg的物块朝相反方向运动，初速度大小都为v=4m/s，它们之间有摩擦．当薄板的速度大小为2.4m/s时，物块的运动情况是（ ）
如图所示，长L=9m的传送带与水平方向的傾角θ=37°，在电动机的带动下以υ=4m/s的速率顺时针方向运行，在传送带的B端有一离传送带很近的挡板P可将传送带上的物块挡住，在传送带的A端无初速地放一质量m=1kg的物块，它与传送带间的动摩擦因数μ=0.5，物块与挡板的碰撞能量损失及碰撞时间不计．（g=10m/s2，sin37°=0.6）求：
（2013?安徽模拟）如图所示，倾角θ=37°的斜面固定在水平面上，一质量M=1kg的物块受平行于斜面向上的轻质橡皮筋拉力． F=9N作用，平行于斜面的轻绳一端固定在物块M上，另一端跨过光滑定滑轮连接A、B两个小物块，物块M处于静止状态．已知物块与斜面间的动摩擦因数μ=0.5，mA=0.2kg，mB=0.3kg，g取l0m/s2．则剪断A、B间轻绳后，关于物块M受到的摩擦力的说法中正确的是（ sin37°=0.6）（ ）
如图所示，有一质量m=1kg的物块，以v=5m/s的初速度开始在水平面上向右滑行．物块运动中始终受到大小为4N、方向水平向左的力F，物块与水平面间的动摩擦因数μ=0.1．求：