题目内容
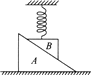
【题目】如图所示，光滑斜面体ABC固定在地面上，斜面AB倾角为37°，斜面AC倾角为53°，P、Q两个物块分别放在AB、AC斜面上，并用绕过斜面体顶端A处光滑定滑轮的细线连接。放在AC斜面上的轻弹簧，一端与Q相连，另一端与固定在C点的挡板相连，物块P、Q的质量分别为2m、m，弹簧的劲度系数为k，重力加速度为g，两斜面足够长。开始时锁定物块P，细线刚好拉直，张力为零，现解除物块P的锁定，已知 sin 37°=0.6，cos 37°= 0.8，求：
(1)解除锁定的一瞬间，物块P的加速度大小；
(2)当物块Q向上运动
的距离时，物块Q的速度大小；
(3)当物块Q向上运动的距离时，弹簧断开，同时给物块P一个平行AB斜面向上的恒定推力F，此后细线的拉力为零，且P、Q两物块的速度同时减为零，则当物块Q速度为零时，物块P克服推力做功为多少。
【答案】（1）0.4g （2）
（3）
【解析】
(1)解除锁定的一瞬间，设物块P的加速度大小为a1；根据牛顿第二定律有
对物块Q研究有
又
解得
a1=0.4g
(2) 由
得开始时弹簧的压缩量
当物块Q向上运动
的距离时，弹簧的伸长量
由此可知，物块Q向上运动的距离时，弹簧的弹性势能变化量为零。根据能量守恒定律可知
可得物块Q的速度大小
(3) 弹簧断开，同时给物块P一个平行AB斜面向上的恒定推力后，物块Q向上做匀减速运动的加速度
物块P向下做匀减速运动的加速度大小也为a2。根据牛顿第二定律有
解得
F=2.8mg
此过程物块Q沿斜面向上运动的距离
物块P克服推力做功
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
