题目内容
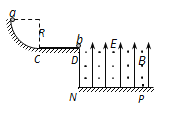
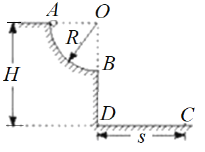
【题目】质谱分析仪中，为解决带电粒子速度方向的发散问题，常使用准直管和偏转电场的小孔相配合的方式。如图甲所示的质谱分析仪中，离子源A产生的初速为零、带电量均为e、质量不同的正离子被电压为U0的加速电场加速后匀速通过准直管，从中轴线上的O点垂直射入匀强偏转电场，偏转后通过极板MN上的小孔S离开电场，经过一段匀速直线运动，垂直于边界O′P进入扇形匀强磁场区域O′PQ。质量为m的正离子恰好能够垂直打在O′Q的中点S1处，已知MO=d，MS=2d，O′T=R，∠PO′Q=90°。（忽略粒子所受重力）求：
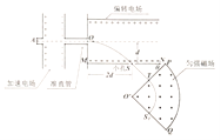
（1）正离子到达O点的动能；
（2）偏转电场场强E0的大小以及MN与O′P的夹角
；
（3）扇形匀强磁场区域的磁感应强度B的大小；
（4）能打在O′Q上的正离子的质量mx的范围；
【答案】（1）
（2）
；45°（3）
（4）
【解析】
（1）动能定理得
（2）正离子被电压为U0的加速电场加速后速度设为v1，对正离子的加速过程应用动能定理
有： 
正离子垂直射入匀强偏转电场，作类平抛运动，加速度设为a，
垂直电场方向匀速运动：
，
沿场强方向匀加速运动：
，
又由速度方向关系可得：
解得θ=45°
电场强度
（3）正离子进入磁场时的速度大小为：
，
正离子在匀强磁场中作匀速圆周运动，由洛伦兹力提供向心力：
，
解得扇形匀强磁场区域的磁感应强度B的大小：
（4）打在O′Q上正离子的轨迹范围如图所示，
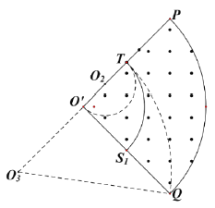
由
解得最大半径
，
同时可得最小半径为
再根据
，由
，
解得。
练习册系列答案
相关题目
