题目内容
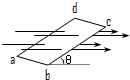一个n匝、面积为S的矩形线框abcd放在磁感应强度为B的水平向右的匀强磁场中，线框平面与水平面的夹角为θ，则穿过的磁通量为（ ）| A、nBScosθ | B、nBSSinθ | C、BSsinθ | D、BScosθ |
分析：线圈在匀强磁场中，当线圈平面与磁场方向垂直时，穿过线圈的磁通量Φ=BS，B是磁感应强度，S是线圈的面积．当线圈平面与磁场方向平行时，穿过线圈的磁通量Φ=0．当存在一定夹角时，则将磁感应强度沿垂直平面方向与平行平面方向分解，从而求出磁通量．
解答：解：线框平面与水平面的夹角为θ，匀强磁场方向水平向右，因此可将磁感应强度沿沿垂直于平面方向分解，所以B⊥=Bsinθ，则穿过矩形线圈的磁通量是Φ=B⊥S=BSsinθ，
故选：C
故选：C
点评：对于匀强磁场中磁通量的求解，可以根据一般的计算公式Φ=BSsinθ（θ是线圈平面与磁场方向的夹角）来分析线圈平面与磁场方向垂直、平行两个特殊情况．
练习册系列答案
相关题目
（2013?商丘三模）如图所示，一个n=10匝，面积为S=0.3m2的圆形金属线圈，其总电阻为R1=2Ω，与R2=4Ω的电阻连接成闭合电路．线圈内存在方向垂直于纸面向里，磁感应强度按B1=2t+3 （T）规律变化的磁场．电阻R2两端通过金属导线分别与电容器C的两极相连．电容器C紧靠着带小孔a（只能容一个粒子通过）的固定绝缘弹性圆筒．圆筒内壁光滑，筒内有垂直水平面竖直向下的匀强磁场B2，O是圆筒的圆心，圆筒的内半径为r=0.4m．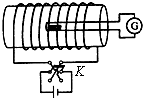
如图所示是测磁感应强度的一种装置．把一个很小的测量线圈放在待测处，测量线圈平面与该处磁场方向垂直，将线圈跟冲击电流计G串联（冲击电流计是一种测量电量的仪器）．当用反向开关K使螺线管里的电流反向时，测量线圈中就产生感应电动势，从而有电流流过G．该测量线圈的匝数为N，线圈面积为S，测量线圈电阻为R，其余电阻不计．
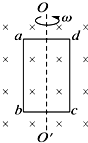如图所示，在磁感应强度为B的匀强磁场中有一个面积为S的矩形N匝线圈绕垂直于磁感线的对称轴OO′以角速度ω匀速转动．