题目内容
 (2013?商丘三模)如图所示,一个n=10匝,面积为S=0.3m2的圆形金属线圈,其总电阻为R1=2Ω,与R2=4Ω的电阻连接成闭合电路.线圈内存在方向垂直于纸面向里,磁感应强度按B1=2t+3 (T)规律变化的磁场.电阻R2两端通过金属导线分别与电容器C的两极相连.电容器C紧靠着带小孔a(只能容一个粒子通过)的固定绝缘弹性圆筒.圆筒内壁光滑,筒内有垂直水平面竖直向下的匀强磁场B2,O是圆筒的圆心,圆筒的内半径为r=0.4m.
(2013?商丘三模)如图所示,一个n=10匝,面积为S=0.3m2的圆形金属线圈,其总电阻为R1=2Ω,与R2=4Ω的电阻连接成闭合电路.线圈内存在方向垂直于纸面向里,磁感应强度按B1=2t+3 (T)规律变化的磁场.电阻R2两端通过金属导线分别与电容器C的两极相连.电容器C紧靠着带小孔a(只能容一个粒子通过)的固定绝缘弹性圆筒.圆筒内壁光滑,筒内有垂直水平面竖直向下的匀强磁场B2,O是圆筒的圆心,圆筒的内半径为r=0.4m.(1)金属线圈的感应电动势E和电容器C两板间的电压U;
(2)在电容器C内紧靠极板且正对a孔的D处有一个带正电的粒子从静止开始经电容器C加速后从a孔垂直磁场B2并正对着圆心O进入筒中,该带电粒子与圆筒壁碰撞四次后恰好又从小孔a射出圆筒.已知粒子的比荷q/m=5×107(C/kg),该带电粒子每次与筒壁发生碰撞时电量和能量都不损失,不计粒子重力和空气阻力,则磁感应强度B2 多大(结果允许含有三角函数式).
分析:(1)根据法拉第电磁感应定律,结合磁感应强度的变化率求出感应电动势的大小.结合闭合电路欧姆定律求出电容器C两板间的电压.
(2)根据动能定理求出粒子进入磁场的速度,结合几何关系求出粒子在磁场中运动的半径与r的关系,结合洛伦兹力提供向心力求出磁感应强度的大小.
(2)根据动能定理求出粒子进入磁场的速度,结合几何关系求出粒子在磁场中运动的半径与r的关系,结合洛伦兹力提供向心力求出磁感应强度的大小.
解答:解:(1)线圈中产生的感应电动势为:E=n
=n
S=100×2×0.03V=6V
电容器C两板间电压为:U=R2
=4V
(2)据动能定理有:qU=
mV2.
带电粒子在磁场中作匀速圆周运动,洛伦兹力提供向心力,有:qVB2=m
.
由于带电粒子与圆筒壁碰撞时无电量和能量损失,那么每次碰撞前后粒子速度大小不变、速度方向总是沿着圆筒半径方向,4个碰撞点与小孔a恰好将圆筒壁五等分,粒子在圆筒内的轨迹具有对称性,由5段相同的圆弧组成,设每段轨迹圆弧对应的圆心角为θ,则由几何关系可得:
=tan(
).
有两种情形符合题意(如图所示):
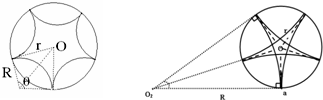
(ⅰ)情形1:每段轨迹圆弧对应的圆心角为:θ=π-
=
.
得:B2=tan
×10-3T
(ⅱ)情形2:每段轨迹圆弧对应的圆心角为:θ′=π-
=
.
将数据代式得:B2=tan(
)×10-3 (T).
答:(1)金属线圈的感应电动势为6V,电容器C两板间的电压为4V.
(2)磁感应强度B2=tan
×10-3T或B2=tan(
)×10-3 (T).
| △φ |
| △t |
| △B |
| △t |
电容器C两板间电压为:U=R2
| E |
| R1+R2 |
(2)据动能定理有:qU=
| 1 |
| 2 |
带电粒子在磁场中作匀速圆周运动,洛伦兹力提供向心力,有:qVB2=m
| V2 |
| R |
由于带电粒子与圆筒壁碰撞时无电量和能量损失,那么每次碰撞前后粒子速度大小不变、速度方向总是沿着圆筒半径方向,4个碰撞点与小孔a恰好将圆筒壁五等分,粒子在圆筒内的轨迹具有对称性,由5段相同的圆弧组成,设每段轨迹圆弧对应的圆心角为θ,则由几何关系可得:
| r |
| R |
| θ |
| 2 |
有两种情形符合题意(如图所示):

(ⅰ)情形1:每段轨迹圆弧对应的圆心角为:θ=π-
| 2π |
| 5 |
| 3π |
| 5 |
得:B2=tan
| 3π |
| 10 |
(ⅱ)情形2:每段轨迹圆弧对应的圆心角为:θ′=π-
| 4π |
| 5 |
| π |
| 5 |
将数据代式得:B2=tan(
| π |
| 10 |
答:(1)金属线圈的感应电动势为6V,电容器C两板间的电压为4V.
(2)磁感应强度B2=tan
| 3π |
| 10 |
| π |
| 10 |
点评:本题考查了电磁感应与电路的综合,以及带电粒子在磁场中运动.对于粒子在磁场中运动,关键确定圆心,根据几何关系确定圆周运动的半径.

练习册系列答案
相关题目
 (2013?商丘三模)如图,MN和PQ是电阻不计的平行金属导轨,其间距为L,导轨弯曲部分光滑,平直部分粗糙,右端接一个阻值为R的定值电阻.平直部分导轨左边区域有宽度为d、方向竖直向上、磁感应强度大小为B的匀强磁场.质量为m、电阻也为R的金属棒从高为h处静止释放,到达磁场右边界处恰好停止.已知金属棒与平直部分导轨间的动摩擦因数为u,金属棒与导轨间接触良好.则金属棒穿过磁场区域的过程中( )
(2013?商丘三模)如图,MN和PQ是电阻不计的平行金属导轨,其间距为L,导轨弯曲部分光滑,平直部分粗糙,右端接一个阻值为R的定值电阻.平直部分导轨左边区域有宽度为d、方向竖直向上、磁感应强度大小为B的匀强磁场.质量为m、电阻也为R的金属棒从高为h处静止释放,到达磁场右边界处恰好停止.已知金属棒与平直部分导轨间的动摩擦因数为u,金属棒与导轨间接触良好.则金属棒穿过磁场区域的过程中( ) (2013?商丘三模)质点做直线运动的位移x和时间平方t2的关系图象如图所示,则该质点( )
(2013?商丘三模)质点做直线运动的位移x和时间平方t2的关系图象如图所示,则该质点( )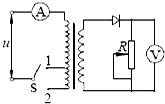 (2013?商丘三模)一台理想变压器,开始时开关S接1,此时原、副线圈的匝数比是11:1,原线圈接入电压为220V的正弦交流电.一只理想二级管和一个滑动变阻器串联接在副线圈上,如图所示.则下列判断正确的是( )
(2013?商丘三模)一台理想变压器,开始时开关S接1,此时原、副线圈的匝数比是11:1,原线圈接入电压为220V的正弦交流电.一只理想二级管和一个滑动变阻器串联接在副线圈上,如图所示.则下列判断正确的是( ) (2013?商丘三模)如图所示,在固定的光滑水平杆(杆足够长)上,套有一个质量为m=0.5kg的光滑金属圆环,轻绳一端拴在环上,另一端系着一个质量为M=1.98kg的木块,现有一质量为m0=20g的子弹以v0=100m/s的水平速度射入木块并留在木块中(不计空气阻力和子弹与木块作用的时间,g取10m/s2),求:
(2013?商丘三模)如图所示,在固定的光滑水平杆(杆足够长)上,套有一个质量为m=0.5kg的光滑金属圆环,轻绳一端拴在环上,另一端系着一个质量为M=1.98kg的木块,现有一质量为m0=20g的子弹以v0=100m/s的水平速度射入木块并留在木块中(不计空气阻力和子弹与木块作用的时间,g取10m/s2),求: