题目内容
如图甲所示，A、B两长方体叠放在一起，放在光滑的水平面上。物体
从静止开始受到一个水平变力的作用，该力与时间的关系如图乙所示，运动过程中A、B始终保持相对静止。则在0~2
时间内，下列说法正确的是（ ）
A．时刻，A、B间的静摩擦力最大，加速度最小
B．时刻，A、B的速度最大
C．0时刻和2时刻，A、B间的静摩擦力最大
D．2时刻，A、B离出发点最远，速度为0
BCD
解析试题分析：以A、B组成的整体作为研究对象，受力分析如图：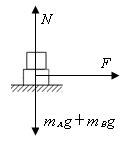
结合牛顿第二定律，可知0~t0时间内A、B组成的整体加速运动，t0~2t0时间内物体保持原来运动方向不变，减速运动，到2t0时刻速度减小到零，距离出发点最远，故Ｂ、Ｄ正确；
对Ａ受力分析如图：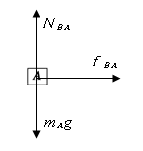
Ｂ对Ａ的摩擦力即为Ａ的合外力，所以Ａ（或整体）加速度越大，ＡＢ间的摩擦力越大，Ａ错C对。
考点：牛顿定律的应用
新题型全程检测期末冲刺100分系列答案如图所示，空间存在一有边界的条形匀强磁场区域，磁场方向与竖直平面（纸面）垂直，磁场边界的间距为L。一个质量为m、边长也为L的正方形导线框沿竖直方向运动，线框所在平面始终与磁场方向垂直，且线框上、下边始终与磁场的边界平行。t＝0时刻导线框的上边恰好与磁场的下边界重合（图中位置Ⅰ），导线框的速度为v0。经历一段时间后，当导线框的下边恰好与磁场的上边界重合时（图中位置Ⅱ），导线框的速度刚好为零。此后，导线框下落，经过一段时间回到初始位置Ⅰ。则
| A．上升过程中，导线框的加速度逐渐增大 |
| B．下降过程中，导线框的加速度逐渐增大 |
| C．上升过程中合力做的功与下降过程中的相等 |
| D．上升过程中克服安培力做的功比下降过程中的多 |
如图所示，小车板面上的物体质量为m＝8kg，它被一根水平方向上拉伸了的弹簧拉住而静止在小车上，这时弹簧的弹力为6N．现沿水平向右的方向对小车施以作用力，使小车由静止开始运动起来，运动中加速度由零逐渐增大到1m/s2，随即以1m/s2的加速度做匀加速直线运动．以下说法正确的是( )
| A．物体受到的摩擦力一直减小 |
| B．物体与小车始终保持相对静止，弹簧对物体的作用力始终没有发生变化 |
| C．当小车加速度(向右)为0.75m/s2时，物体不受摩擦力作用 |
| D．小车以1m/s2的加速度向右做匀加速直线运动时，物体受到的摩擦力为8N |
如图所示，A为系在竖直轻弹簧上的小球，在竖直向下的恒力F的作用下，弹簧被压缩到B点，现突然撤去力F，小球将在竖直方向上开始运动，若不计空气阻力，则下列中说法正确的是 （ ）
| A．撤去F后小球，地球，弹簧构成的系统机械能守恒； |
| B．小球在上升过程中，弹性势能先减小后增大； |
| C．小球在上升过程中，弹簧的形变量恢复到最初（指撤去力F的瞬间）的一半时，小球的动能最大； |
| D．小球在上升过程中，动能先增大后减小； |
如图，物体将轻质弹簧压缩后由静止释放，物体在弹力的推动下沿粗糙水平面向右运动，不计空气阻力，物体从开始运动到与弹簧分离的全过程中
| A．物体做匀加速运动 |
| B．物体的加速度的大小逐渐减小 |
| C．物体的速度先增大后减小 |
| D．物体与弹簧分离时速度最大 |
某游乐场开发了一个名为“翻天滚地”的游乐项目。原理图如图所示：一个
圆弧形光滑圆管轨道ABC，放置在竖直平面内，轨道半径为R，在A 点与水平地面AD相接，地面与圆心O等高，MN 是放在水平地面上长为3R、厚度不计的减振垫，左端M正好位于A点．让游客进入一个中空的透明弹性球，人和球的总质量为m，球的直径略小于圆管直径。将球（内装有参与者）从A处管口正上方某处由静止释放后，游客将经历一个“翻天滚地”的刺激过程。不考虑空气阻力，弹性球可看作质点。那么以下说法中正确的是 （ ）
A．要使球能从C点射出后能打到垫子上，则球经过C点时的速度至少为 |
B．要使球能从C点射出后能打到垫子上，则球经过C点时的速度至少为 |
C．若球从C点射出后恰好能打到垫子的M端，则球经过C点时对管的作用力大小为 |
D．要使球能通过C点落到垫子上，球离A点的最大高度是 |
如图所示，劲度系数为k的轻质弹簧，一端系在竖直放置的半径为R的圆环顶点P，另一端系一质量为m的小球，小球穿在圆环上做无摩擦的运动。设开始时小球置于A点，弹簧处于自然状态，当小球运动到最低点时速率为v，对圆环恰好没有压力。下列分析正确的是（ ）
| A．从A到B的过程中,小球的机械能守恒 |
| B．从A到B的过程中,小球的机械能增加 |
C．小球过B点时,弹簧的弹力为mg+ |
| D．小球过B点时,弹簧的弹力为mg－ |
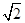m/s
m/s