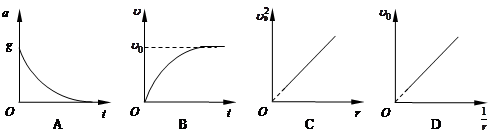题目内容
某游乐场开发了一个名为“翻天滚地”的游乐项目。原理图如图所示:一个 圆弧形光滑圆管轨道ABC,放置在竖直平面内,轨道半径为R,在A 点与水平地面AD相接,地面与圆心O等高,MN 是放在水平地面上长为3R、厚度不计的减振垫,左端M正好位于A点.让游客进入一个中空的透明弹性球,人和球的总质量为m,球的直径略小于圆管直径。将球(内装有参与者)从A处管口正上方某处由静止释放后,游客将经历一个“翻天滚地”的刺激过程。不考虑空气阻力,弹性球可看作质点。那么以下说法中正确的是 ( )
圆弧形光滑圆管轨道ABC,放置在竖直平面内,轨道半径为R,在A 点与水平地面AD相接,地面与圆心O等高,MN 是放在水平地面上长为3R、厚度不计的减振垫,左端M正好位于A点.让游客进入一个中空的透明弹性球,人和球的总质量为m,球的直径略小于圆管直径。将球(内装有参与者)从A处管口正上方某处由静止释放后,游客将经历一个“翻天滚地”的刺激过程。不考虑空气阻力,弹性球可看作质点。那么以下说法中正确的是 ( )
A.要使球能从C点射出后能打到垫子上,则球经过C点时的速度至少为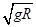 |
B.要使球能从C点射出后能打到垫子上,则球经过C点时的速度至少为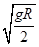 |
C.若球从C点射出后恰好能打到垫子的M端,则球经过C点时对管的作用力大小为 |
D.要使球能通过C点落到垫子上,球离A点的最大高度是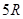 |
BCD
解析试题分析:小球离开C点做平抛运动,落到M点时水平位移为R,竖直下落高度为R,根据运动学公式可得:
R=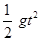 ,运动时间t=
,运动时间t= ,从C点射出的速度为v1=
,从C点射出的速度为v1=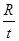 =
=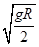 ,所以,A错B对;设小球以v1经过C点受到管子对它的作用力为FN,由向心力公式可得:mg-FN=
,所以,A错B对;设小球以v1经过C点受到管子对它的作用力为FN,由向心力公式可得:mg-FN=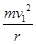 ,解得, FN=
,解得, FN= ,所以C正确;小球下降的高度最高时,小球运动的水平位移为4R,打到N点.设能够落到N点的水平速度为v2,根据平抛运动求得:v2=
,所以C正确;小球下降的高度最高时,小球运动的水平位移为4R,打到N点.设能够落到N点的水平速度为v2,根据平抛运动求得:v2=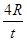 =
=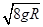 ,设小球下降的最大高度为H,根据机械能守恒定律可知:mg(H-R)=
,设小球下降的最大高度为H,根据机械能守恒定律可知:mg(H-R)= ,解得H=5R,所以D正确。
,解得H=5R,所以D正确。
考点:机械能守恒定律;牛顿第二定律;平抛运动;向心力.

练习册系列答案
相关题目
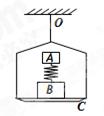
如图所示,滑轮A可沿倾角为θ的足够长光滑轨道下滑,滑轮下用轻绳挂着一个重为G的物体B,下滑时,物体B相对于A静止,则下滑过程中 ( )
| A.B的加速度为gsinθ |
B.绳的拉力为 |
| C.绳的方向保持竖直 |
| D.绳的拉力为G |
今年我省许多地区出现罕见的干旱,在一次向云层发射溴化银炮弹进行人工增雨作业的过程中,下列说法正解的是( )
| A.炮弹向上运动的过程中克服摩擦力做负功 |
| B.炮弹向上运动的过程中机械能守恒 |
| C.炮弹向上运动时加速度大于向下运动时的加速度 |
| D.炮弹向上运动的过程中机械能增加 |
一小球从空中由静止下落,已知下落过程中小球所受阻力与速度的平方成正比,设小球离地足够高,则 ( )
| A.小球在做减速运动 | B.小球一直在做加速运动 |
| C.小球先加速后匀速 | D.小球先加速后减速 |
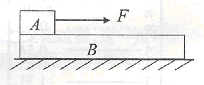
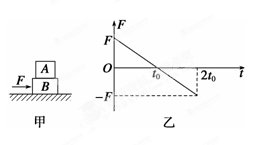
 从静止开始受到一个水平变力的作用,该力与时间的关系如图乙所示,运动过程中A、B始终保持相对静止。则在0~2
从静止开始受到一个水平变力的作用,该力与时间的关系如图乙所示,运动过程中A、B始终保持相对静止。则在0~2 时间内,下列说法正确的是( )
时间内,下列说法正确的是( )