题目内容
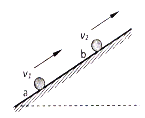
【题目】如图所示,一倾角为30°的足够长光滑斜面上有两个质量相等的小球a和b,开始时两小球相距x0=0.6m,且以初速度v1=5m/s、v2=2m/s沿斜面向上运动,球a追上b球发生碰撞,碰撞时间极短且无机械能的损失。g取10m/s2,试求:
(1)碰撞点的位置与b球初始位置的距离
(2)当b球上升至最高点时,两球间的距离
【答案】(1)0.3m(2)1m/s,4m/s
【解析】(1)因斜面光滑,所以两球加速度相同, a1=a2=gsin30°=5m/s2
设经时间t,球a追上b,两球发生碰撞,由位移关系得
带入数据解得: ![]()
解得t=0.2s
所以碰撞点的位置与b球初始位置的距离x=![]() =0.3m
=0.3m
(2)设两球相撞时的速度分别为v10、v20,则
![]() ,
, ![]()
设两球质量为m,碰撞后的速度分别为v1′,v2′
由动量守恒得 mv10+mv20= mv1′+m v2′
由于碰撞无机械能损失,所以![]()
带入数据解得v1′=1m/s ,v2′=4m/s;

练习册系列答案
相关题目
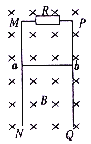
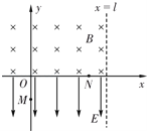
【题目】如图所示,足够长的光滑平行金属导轨MN、PQ竖直放置,一匀强磁场垂直穿过导轨平面,导轨的上端M与P之间连接阻值为R=0.40Ω的电阻,质量为m=0.01kg、电阻为r=0.30Ω的金属棒ab紧贴在导轨上。现使金属棒ab由静止开始自由下滑,其下滑距离与时间的关系如下图所示,导轨电阻不计,重力加速度g取10m/s2。
试求:
时间t(s) | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 |
下滑距离s(m) | 0 | 0.1 | 0.3 | 0.7 | 1.4 | 2.1 | 2.8 | 3.5 |
(1)当t=0.7s时,重力对金属棒ab做功的功率;
(2)金属棒ab在开始运动的0.7s内,电阻R上产生的焦耳热;
(3)从开始运动到t=0.4s的时间内,通过金属棒ab的电荷量。