题目内容
14.在高速公路上常用超声波测速仪测量汽车的速度,测速仪是根据它发出并接收超声波脉冲信号时间差来测出汽车速度的.设超声波测速仪发出的脉冲信号的时间间隔为1s,超声波在空气中传播的速度是340m/s.若汽车静止时,超声波测速仪所接收到的脉冲信号的时间间隔也为1s.问:(1)当超声波测速仪所接收到的脉冲信号的时间间隔大于1s时,你能判定汽车是做怎样的运动吗?反之又怎样?
(2)若这一时间间隔为1.2s,则汽车行驶的速度是多少?
分析 超声波信号从发出到被反射回来的时间间隔△t=$\frac{2s}{{v}_{0}}$,在该时间段内,超声波匀速前进,汽车也是匀速前进,在$\frac{s}{{t}_{0}}$时刻两者相遇;根据速度定义式求解即可.
解答 解:(1)设第一次超声波信号从发出到被反射回来的时间间隔△t1,第二次超声波信号从发出到被反射回来的时间间隔△t2,第一次放出的超声波与汽车相遇时超声波前进距离为:x1=v声•$\frac{1}{2}$△t1…①
第二次放出的超声波与汽车相遇时超声波前进距离为:x2=v声•$\frac{1}{2}$△t2…②
若汽车静止,则x1=x2,△t1=△t2,超声波测速仪所接收到的脉冲信号的时间间隔也为1s.
当超声波测速仪所接收到的脉冲信号的时间间隔大于1s时,△t2>△t1,结合①②可得:x2>x1,所以汽车远离超声波测速仪;
反之,当超声波测速仪所接收到的脉冲信号的时间间隔小于1s时,△t2<△t1,结合①②可得:x2<x1,所以汽车向超声波测速仪运动.
(2)超声波测速仪所接收到的脉冲信号的时间间隔为1.2s时,两次脉冲运动的时间差:△t2-△t1=1.2-1.0=0.2s
汽车运动的时间:$t=1+\frac{△{t}_{2}-△{t}_{1}}{2}=1+0.1=1.1$s
则汽车在1.1s内的位移:△x=x2-x1=$\frac{1}{2}{v}_{声}•(△{t}_{2}-△{t}_{1})$=$\frac{1}{2}×340×(1.2-1.0)=34$m
所以汽车的速度:$v=\frac{△x}{t}=\frac{34}{1.1}≈30$m/s
答:(1)当超声波测速仪所接收到的脉冲信号的时间间隔大于1s时汽车远离超声波测速仪,反之汽车向超声波测速仪运动.
(2)若这一时间间隔为1.2s,则汽车行驶的速度是30m/s.
点评 本题关键是通过声波的发射和接收过程;由于超声波的速度不变,故一定可以得出超声波前进和返回过程的时间是相等的.

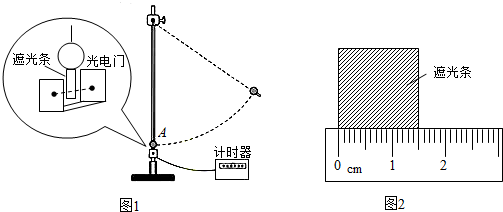
(1)用△Ep=mgh计算钢球重力势能变化的大小,式中钢球下落高度h应测量释放时的钢球球心到B之间的竖直距离.
(A)钢球在A点时的顶端
(B)钢球在A点时的球心
(C)钢球在A点时的底端
(2)用△Ek=$\frac{1}{2}$mv2计算钢球动能变化的大小,用刻度尺测量遮光条宽度,示数如图2所示,其读数为1.50cm.某次测量中,计时器的示数为0.0100s,则钢球的速度为v=1.50m/s.
(3)如表为该同学的实验结果:
他发现表中的△Ep与△Ek之间存在差异,你认为这是所测量速度为挡光片的速度,比小球速度大造成的.应该如何修正测出固定点到挡光片的距离算出小球速度即可.
| △Ep(×10-2J) | 4.892 | 9.786 | 14.69 | 19.59 | 29.38 |
| △Ek(×10-2J) | 5.04 | 10.1 | 15.1 | 20.0 | 29.8 |
 如图所示电路图中,电源内阻不能忽略,R1=10Ω,R2=8Ω.当开关S板到位置1时,电压表的读数为2.0V,当开关S板到位置2时,电压表的读数可能是( )
如图所示电路图中,电源内阻不能忽略,R1=10Ω,R2=8Ω.当开关S板到位置1时,电压表的读数为2.0V,当开关S板到位置2时,电压表的读数可能是( )| A. | 2.2V | B. | 1.9V | C. | 1.6V | D. | 1.4V |
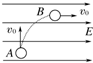 带电粒子以速度v0沿竖直方向垂直进入匀强电场E中,如图所示,经过一段时间后,其速度变为水平方向,大小仍为v0,则一定有( )
带电粒子以速度v0沿竖直方向垂直进入匀强电场E中,如图所示,经过一段时间后,其速度变为水平方向,大小仍为v0,则一定有( )| A. | 电场力与重力大小相等 | |
| B. | 粒子运动的水平位移大小等于竖直位移大小 | |
| C. | 电场力所做的功一定等于重力做的功的负值 | |
| D. | 电势能的减少量一定等于重力势能的增加量 |
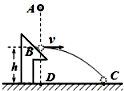 如图所示,从A点由静止释放一小球,一段时间后与固定斜面上B点发生碰撞,碰后小球速度大小不变,方向变为水平方向,又经过相同时间落于地上C点,已知地面上D点位于B点正下方,B、D间距离为h,则( )
如图所示,从A点由静止释放一小球,一段时间后与固定斜面上B点发生碰撞,碰后小球速度大小不变,方向变为水平方向,又经过相同时间落于地上C点,已知地面上D点位于B点正下方,B、D间距离为h,则( )| A. | AB两点间距离为h | B. | AB两点间距离为$\frac{h}{2}$ | ||
| C. | CD两点间距离为h | D. | CD两点间距离为$\sqrt{2}$h |
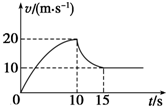 某跳伞运动员从悬停在高空的直升机上跳下,他从跳离飞机到落地的过程中在空中沿竖直方向运动的v-t图象如图所示,则下列关于他的运动情况分析正确的是( )
某跳伞运动员从悬停在高空的直升机上跳下,他从跳离飞机到落地的过程中在空中沿竖直方向运动的v-t图象如图所示,则下列关于他的运动情况分析正确的是( )| A. | 0~10 s加速度向下,10 s~15 s加速度向上 | |
| B. | 0~10 s、10 s~15 s内都在做加速度逐渐减小的变速运动 | |
| C. | 0~10 s内下落的距离大于100 m | |
| D. | 10 s~15 s内下落的距离大于75 m |
 (1)在“验证机械能守恒定律”实验中,在下面所列举的该实验的几个操作步骤中,你认为没有必要进行的或者错误的步骤是BCD(填字母代号)
(1)在“验证机械能守恒定律”实验中,在下面所列举的该实验的几个操作步骤中,你认为没有必要进行的或者错误的步骤是BCD(填字母代号)