题目内容
3.A、B两列火车在同一轨道上同向行驶,A在前,速度为vA=10m/s,B车在后,速度vB=30m/s.因大雾能见度低,B车在距A车487.5m时,才发现前方有A车,这时B车立即刹车,如果前方没有任何障碍物,B车还要滑行1800m才能停止.问:A车若仍按原速前进,两车是否会相撞(写出具体判断过程)?若会相撞,将在B刹车后多长时间相撞?分析 第一问根据题意先求B车的加速度,再求B车的刹车距离和在相同时间内A车通过的距离,再判断辆车是否相撞;第二问根据A车通过的距离与B车刹车时的距离之和等于B车通过的距离列式求解.
解答 解:B车的加速度为:${a}_{B}=\frac{{{v}_{B}}^{2}}{2{s}_{B}}=\frac{{30}^{2}}{2×1800}m/{s}^{2}=0.25m/{s}^{2}$
当B的速度等于A的速度时有:${s}_{B}=\frac{{{v}_{B}}^{2}-{{v}_{A}}^{2}}{2{a}_{B}}=\frac{{30}^{2}-{10}^{2}}{2×0.25}m=1600m$
运动时间为:$t=\frac{{v}_{B}-{v}_{A}}{{a}_{B}}=\frac{30-10}{0.25}s=80s$
在这段时间内火车A通过的距离为:sA=vAt=10×80m=800m
因为sB-sA=800m>487.5m,所以会相撞
设相撞时间为t1,则有:${v}_{A}{t}_{1}+{s}_{1}={v}_{B}{t}_{1}-\frac{1}{2}{{at}_{1}}^{2}$,
即:$10m/s×{t}_{1}+487.5m=30m/s×{t}_{1}-\frac{1}{2}×0.25m/{s}^{2}×{{t}_{1}}^{2}$,
解之得:t1=30s
答:A车若仍按原速前进,两车会相撞,且在刹车后30s时间内相撞.
点评 解答本题的关键在于判断两车相撞的条件,即B车行驶的距离大于B车刹车时的距离与A车行驶距离的和,然后结合匀变速直线运动的相关公式解答即可.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
13.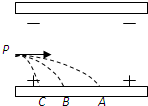 如图所示,有三个质量相等分别带正电、负电和不带电的小球,从平行板电场中的P点以相同的初速度垂直于电场方向进入电场,它们分别落到A、B、C三点,则可以断定( )
如图所示,有三个质量相等分别带正电、负电和不带电的小球,从平行板电场中的P点以相同的初速度垂直于电场方向进入电场,它们分别落到A、B、C三点,则可以断定( )
 如图所示,有三个质量相等分别带正电、负电和不带电的小球,从平行板电场中的P点以相同的初速度垂直于电场方向进入电场,它们分别落到A、B、C三点,则可以断定( )
如图所示,有三个质量相等分别带正电、负电和不带电的小球,从平行板电场中的P点以相同的初速度垂直于电场方向进入电场,它们分别落到A、B、C三点,则可以断定( )| A. | 落到A点的小球带正电,落到B点的小球不带电,落到C点的小球带负电 | |
| B. | 三小球在电场中运动时间相等 | |
| C. | 三小球到达正极板的动能关系:EKA>EKB>EKC | |
| D. | 三小球在电场中运动的加速度关系:aA>aB>aC |
11.以v0=12m/s的速度匀速行驶的汽车,突然刹车做匀减速直线运动,刹车过程汽车加速度大小为6m/s2,则刹车后( )
| A. | 2 s末停止运动 | B. | 3 s内的位移是9 m | ||
| C. | 1 s末速度的大小是18 m/s | D. | 3 s末速度的大小是6 m/s |
18.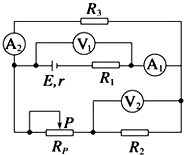 如图所示,图中的四个电表均为理想电表,当滑动变阻器滑片P向右端移动时,下面说法中正确的是( )
如图所示,图中的四个电表均为理想电表,当滑动变阻器滑片P向右端移动时,下面说法中正确的是( )
 如图所示,图中的四个电表均为理想电表,当滑动变阻器滑片P向右端移动时,下面说法中正确的是( )
如图所示,图中的四个电表均为理想电表,当滑动变阻器滑片P向右端移动时,下面说法中正确的是( )| A. | 电压表V1的读数减小,电流表A1的读数增大 | |
| B. | 电压表V1的读数增大,电流表A1的读数减小 | |
| C. | 电压表V2的读数减小,电流表A2的读数增大 | |
| D. | 电压表V2的读数增大,电流表A2的读数减小 |
8.某一做匀加速直线运动物体的加速度为3m/s2.对于运动过程中的任意ls来说,下列说法正确的是( )
| A. | 物体在这ls末的速度比这ls初的速度总是大3m/s | |
| B. | 物体在这ls末的速度比这ls初的速度总是大3倍 | |
| C. | 物体在这ls末的速度一定比前ls末的速度大 3m/s | |
| D. | 物体在这ls末的速度一定比前ls初的速度大6m/s |
15.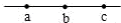 如图所示,一条电场线上有a、b、c三点,b为ac连线的中点,a、c两点的电势分别为φa=-4V,φc=-6V.下列说法正确的是( )
如图所示,一条电场线上有a、b、c三点,b为ac连线的中点,a、c两点的电势分别为φa=-4V,φc=-6V.下列说法正确的是( )
 如图所示,一条电场线上有a、b、c三点,b为ac连线的中点,a、c两点的电势分别为φa=-4V,φc=-6V.下列说法正确的是( )
如图所示,一条电场线上有a、b、c三点,b为ac连线的中点,a、c两点的电势分别为φa=-4V,φc=-6V.下列说法正确的是( )| A. | b点的电势为-5V | |
| B. | a点的场强大于c点的场强 | |
| C. | 电场线的方向由a指向c | |
| D. | 正电荷由b点的电势能比在c点的电势能大 |
13.甲、乙两物体在t=0时的位置如图(a)所示,之后它们沿x轴正方向运动的速度图象如图(b)所示,则以下说法正确的有( )
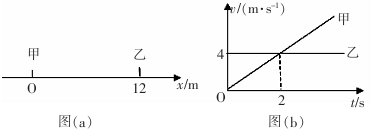

| A. | t=2s时甲追上乙 | |
| B. | 在前4s内甲乙两物体位移相等 | |
| C. | 甲追上乙之前两者间的最远距离为4m | |
| D. | 甲追上乙时的速度大小为8m/s |