Question

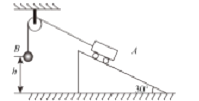
【题目】如图所示，小车A放在一个倾角为30°的足够长的固定的光滑斜面上，A、B两物体由绕过轻质定滑轮的细线相连，已知重力加速度为g，滑轮质量及细线与滑轮之间的摩擦不计，小车A的质量为3m，小球B的质量为m，小车从静止释放后，在小球B竖直上升h的过程中(小球B未到达滑轮处)，小车受绳的拉力大小T和小车获得的动能Ek分别为( )

A. T＝mg，Ek＝mgh

B. T＝mg，Ek＝mgh

C. T＝mg，Ek＝mgh

D. T＝mg，Ek＝mgh

Answer 1

【答案】D

【解析】小车A与小球B构成的系统做加速运动，隔离分析小车，据牛顿第二定律得：3mgsin30°-FT=3ma
隔离分析小球B，据牛顿第二定律得：FT-mgsin30°=ma
联立可得小车受绳的拉力大小：
当小球B上升h高度时，根据动能定理有：3mghsin30°-mgh=(3m+m)v2
解得：

小车的最大动能为：，综合上述可知，故ABC错误，D正确．
故选D．