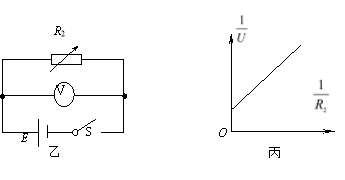
题目内容
【题目】如图所示，有三个斜面a、b、c，底边的长分别为L、L、2L，高度分别为2h、h、h，某物体与三个斜面间的动摩擦因数都相同，这个物体分别沿三个斜面从顶端由静止下滑到底端．三种情况相比较，下列说法正确的是( )
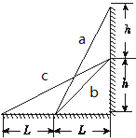
A. 物体损失的机械能ΔEc＝2ΔEb＝4ΔEa
B. 因摩擦产生的热量2Qa＝2Qb＝Qc
C. 物体到达底端的动能Eka＝2Ekb＝2Ekc
D. 因摩擦产生的热量4Qa＝2Qb＝Qc
【答案】B
【解析】设斜面和水平方向夹角为θ，斜面长度为X，则物体下滑过程中克服摩擦力做功为：W=mgμXcosθ，Xcosθ即为底边长度．物体下滑，除重力外有摩擦力做功，根据能量守恒，损失的机械能 转化成摩擦产生的内能．由图可知a和b底边相等且等于c的一半，故摩擦生热关系为：Qa=Qb=
Qc，所以损失的机械能△Ea=△Eb=△Ec，故A错误．由图可知a和b底边相等且等于c的，克服摩擦力所做功等于因摩擦产生热量，故摩擦生热关系为：Qa=Qb=Qc，即：2Qa=2Qb=Qc，故B正确，D错误．设物体滑到底端时的速度为v，根据动能定理得：mgH-mgμXcosθ=mv2-0，Eka=2mgh-mgμL，Ekb=mgh-mgμL，Ekc=mgh-mgμ2L，根据图中斜面高度和底边长度可知滑到底边时动能大小关系为：Eka＞EKb＞Ekc，故C错误．故选B．
练习册系列答案
相关题目
