题目内容
4.如图所示,两块很大的平行导体板MN、PQ产生竖直向上的匀强电场,两平行导体板与一半径为r的单匝线圈连接,在线圈内有一方向垂直线圈平面向里,磁感应强度变化率为$\frac{△{B}_{1}}{△t}$的匀强磁场.在两导体板之间还存在有理想边界的匀强磁场,匀强磁场分布为I、II两个区域,其边界为MN、ST、PQ,磁感应强度大小均为B2,方向如图所示,I区域高度为d1,II区域的高度为d2.一个质量为m、电量为q的带正电的小球从MN板上方的O点由静止开始下落,穿过MN板的小孔进入复合场后,恰能做匀速圆周运动,II区域的高度d2足够大,带电小球在运动中不会与PQ板相碰,重力加速度为g.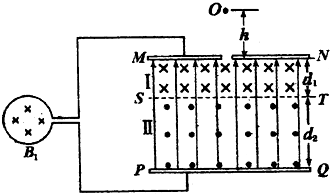
(1)求线圈内匀强磁场的磁感应强度变化率$\frac{△{B}_{1}}{△t}$;
(2)若带电小球运动后恰能回到O点,求带电小球释放时距MN的高度h;
(3)若带电小球从距MN的高度为3h的O’点由静止开始下落,为使带电小球运动后仍能回到O’点,在磁场方向不改变的情况下对两导体板之间的匀强磁场作适当的调整,请你设计出两种方案并定量表示出来.
分析 (1)小球能做匀速圆周运动,则有电场力与重力平衡,根据平衡条件求解出电场强度后,根据法拉第电磁感应定律求解线圈内匀强磁场的磁感应强度变化率;
(2)只有小球从进入磁场的位置离开磁场,做竖直上抛运动,才能恰好回到O点;结合对称性,画出运动轨迹,根据几何关系,结合动能定理与牛顿第二定律,即可求解;
(3)由上式高度可知,从而确定磁感应强度的变化值,并依重力与电场力相等,从而确定距离关系.
解答 解:(1)带电小球进入复合场后恰能做匀速圆周运动,则电场力与重力平衡,得:
qE=mg
根据公式U=Ed得到:
E=$\frac{U}{{d}_{1}+{d}_{2}}$
根据法拉第电磁感应定律,有:
U=$\frac{△{B}_{1}}{△t}$=πr2
解得:
$\frac{△{B}_{1}}{△t}$=$\frac{mg({d}_{1}+{d}_{2})}{qπ{r}^{2}}$
(2)只有小球从进入磁场的位置离开磁场,做竖直上抛运动,才能恰好回到O点,由于两个磁场区的磁感应强度大小都相等,所以半径都为R,由图可知△O1O2O3是等边三角形.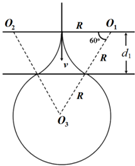
根据动能定理,有:
mgh=$\frac{1}{2}$mv2
根据洛伦兹力提供向心力,有:
qvB2=m$\frac{{v}^{2}}{R}$
三个圆心的连线构成等边三角形,结合几何关系,有:
R=$\frac{2}{3}\sqrt{3}$d1
解得:h=$\frac{2{d}_{1}^{2}{q}^{2}{B}_{2}^{2}}{3g{m}^{2}}$
(3)方案1:改变磁感应强度
自由落体过程,根据动能定理,有:
mg×3h=$\frac{1}{2}$m${v}_{1}^{2}$
解得:v1=$\sqrt{6gh}$=$\sqrt{3}$v
根据洛伦兹力提供向心力,有:
qv1′B2′=m$\frac{{v}_{1}^{2}}{R}$
B2′=$\sqrt{3}$B2
将两板之间的匀强磁场的磁感应强度增大为原来的$\sqrt{3}$倍.
方案2:改变磁场的宽度:
由h=$\frac{2{d}_{1}^{2}{q}^{2}{B}_{2}^{2}}{3g{m}^{2}}$可知,将磁场I区的宽度增大为原来的$\sqrt{3}$倍,即d1′=$\sqrt{3}$d1.
磁场II区的宽度变为d2′=d2-($\sqrt{3}$-1)d1
方案3:改变磁场边界:磁场II区的磁场边界下移y的距离.
当带电小球从距MN的高度为3h的O′点由静止开始下落时,应有
mg×3h=$\frac{1}{2}$m${v}_{1}^{2}$
根据洛伦兹力提供向心力,有:
qv1B2=m$\frac{{v}_{1}^{2}}{R}$
由第2问解析,有:
h=$\frac{2{d}_{1}^{2}{q}^{2}{B}_{2}^{2}}{3g{m}^{2}}$
R1=2d1
画出粒子的运动轨迹,如右图所示,在中间匀速直线运动过程中,粒子的速度方向与竖直方向成30°角,根据几何关系,可得
y=$\frac{{R}_{1}cos30°-R{\;}_{1}(1-cos30°)}{tan30°}$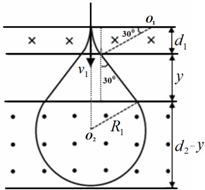
y=(6-2$\sqrt{3}$)d1
方案4:同时改变磁感应强度和磁场边界(上图中300角改为θ角)
设磁感应强度增大k倍.B2′=kB2
则磁场II区域的上边界下移y的距离
y=$\frac{{R}_{1}cosθ-{R}_{1}(1-cosθ)}{tanθ}$
式中:R1=$\frac{2{d}_{1}}{k}$
cosθ=$\sqrt{1-(\frac{1}{2}k)^{2}}$
tanθ=$\frac{1}{\sqrt{\frac{4}{{k}^{2}}-1}}$
答:(1)线圈内匀强磁场的磁感应强度变化率为$\frac{mg({d}_{1}+{d}_{2})}{qπ{r}^{2}}$;
(2)若带电小球运动后恰能回到O点,带电小球释放时距MN的高度h为$\frac{2{d}_{1}^{2}{q}^{2}{B}_{2}^{2}}{3g{m}^{2}}$;
(3)方案如上所示.
点评 考查带电小球在复合场中做运动,结合受力分析,掌握物理规律,形成解题思路,提高分析问题的能力.

 寒假学与练系列答案
寒假学与练系列答案| A. | 一定是直线运动 | B. | 一定是曲线运动 | C. | 可能是圆周运动 | D. | 可能是平抛运动 |
 如图所示,质量为10kg的物块A拴在一个被水平拉伸的弹簧一端,弹簧的拉力为4N时,物体A和小车均处于静止状态,现使小车以1m/s2的加速度运动,设物体受到的最大静摩擦力等于滑动摩擦力,g=10m/s2,则下列说法正确的是( )
如图所示,质量为10kg的物块A拴在一个被水平拉伸的弹簧一端,弹簧的拉力为4N时,物体A和小车均处于静止状态,现使小车以1m/s2的加速度运动,设物体受到的最大静摩擦力等于滑动摩擦力,g=10m/s2,则下列说法正确的是( )| A. | 若加速度方向水平向右,则物体A相对小车一定向左发生滑动 | |
| B. | 若加速度方向水平向右,则物体A与小车相对静止时受到的摩擦力一定等于6N | |
| C. | 若加速度方向水平向左,则物体A与小车相对静止时受到的摩擦力与弹簧的弹力可能相等 | |
| D. | 若加速度方向水平向左,则物体A与小车相对静止时弹簧的弹力可能为8N |

| A. | v=7.9km/s是第一宇宙速度,是飞行器在地球周围空间飞行的最大速度 | |
| B. | v=11.2km/s是第二宇宙速度,以该速度发射的飞行器可以克服地球引力离开地球 | |
| C. | v=16.7km/s是第三宇宙速度,以该速度发射的飞行器可以挣脱太阳引力的束缚,飞到太阳系外 | |
| D. | 当发射速度介于v=7.9km/s与v=11.2km/s之间时,飞行器将绕地球在更高轨道上做圆周运动 |
 如图所示是甲乙两物体从同一点出发的位移-时间(x-t)图象,由图象可以看出在0〜4s这段时间内( )
如图所示是甲乙两物体从同一点出发的位移-时间(x-t)图象,由图象可以看出在0〜4s这段时间内( )| A. | 甲、乙两物体始终同向运动 | B. | 4s时甲、乙两物体之间的距离最大 | ||
| C. | 甲的平均速度等于乙的平均速度 | D. | 甲、乙两物体之间的最大距离为4m |
 纪念中国人民抗日战争暨世界反法西斯战争胜利70周年阅兵式于2015年9月3日在北京天安门广场举行,参加阅兵的履带步兵战车方队是履带装备方队中承载员最多的方队.他们驾驶04A型履带步兵战车第3个通过天安门,该步兵战车作为装甲步兵信息化条件下机动突击作战的新型主战装备,首次亮相阅兵,在某次训练过程中,重2.5×104kg的04A型履带步兵战车以加速度0.6m/s2恒定启动.已知其运行过程中所受阻力恒定为其重力的0.1倍.其匀加速至额定功率400kW后维持额定功率不变加速到最大速度,从启动到最大速度总用时为$\frac{100}{3}$s.求:
纪念中国人民抗日战争暨世界反法西斯战争胜利70周年阅兵式于2015年9月3日在北京天安门广场举行,参加阅兵的履带步兵战车方队是履带装备方队中承载员最多的方队.他们驾驶04A型履带步兵战车第3个通过天安门,该步兵战车作为装甲步兵信息化条件下机动突击作战的新型主战装备,首次亮相阅兵,在某次训练过程中,重2.5×104kg的04A型履带步兵战车以加速度0.6m/s2恒定启动.已知其运行过程中所受阻力恒定为其重力的0.1倍.其匀加速至额定功率400kW后维持额定功率不变加速到最大速度,从启动到最大速度总用时为$\frac{100}{3}$s.求: 如图所示,在xOy平面内,x轴上方有沿y轴向上的足够大的匀强电场,电场的下边界为y1=0.5m的直线,在y轴上y2=1.0m处有一放射源S,x轴上有一个足够大的荧光屏,放射源S在如图180°范围内,发射初速度v0=200m/s的电子,整个装置放在真空中,已知场强大小为9.3×10-7V/m,电子质量为9.3×10-31kg,电量为1.6×10-19C求:
如图所示,在xOy平面内,x轴上方有沿y轴向上的足够大的匀强电场,电场的下边界为y1=0.5m的直线,在y轴上y2=1.0m处有一放射源S,x轴上有一个足够大的荧光屏,放射源S在如图180°范围内,发射初速度v0=200m/s的电子,整个装置放在真空中,已知场强大小为9.3×10-7V/m,电子质量为9.3×10-31kg,电量为1.6×10-19C求: 如图为一个利用电场、磁场对电荷运动控制的模型图.在区域I中的P1、P2分别为加速电场的正负两极板,P2中央有一孔,两极板竖直平行正对放置,开始加有大小为U的电压;在区域Ⅱ中有一以l及l′为边界的竖直向下的匀强电场;在区域Ⅲ中有一以l′为左边界垂直于纸面的匀强磁场.现有一带正电的粒子(重力不计)质量为m,电量为q,从极板P1由静止开始沿中轴线OO′方向进入区域Ⅱ,从边界l′的P点离开区域Ⅱ,此时速度与水平方向夹角α=30°.若将P1、P2两极板所加电压改为U′,其它条件不变,粒子则从边界l′的Q点离开区域Ⅱ,此时速度与水平方向夹角β=60°.已知PQ两点的距离为d.
如图为一个利用电场、磁场对电荷运动控制的模型图.在区域I中的P1、P2分别为加速电场的正负两极板,P2中央有一孔,两极板竖直平行正对放置,开始加有大小为U的电压;在区域Ⅱ中有一以l及l′为边界的竖直向下的匀强电场;在区域Ⅲ中有一以l′为左边界垂直于纸面的匀强磁场.现有一带正电的粒子(重力不计)质量为m,电量为q,从极板P1由静止开始沿中轴线OO′方向进入区域Ⅱ,从边界l′的P点离开区域Ⅱ,此时速度与水平方向夹角α=30°.若将P1、P2两极板所加电压改为U′,其它条件不变,粒子则从边界l′的Q点离开区域Ⅱ,此时速度与水平方向夹角β=60°.已知PQ两点的距离为d.