��Ŀ����
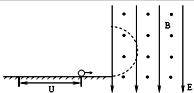
9�� ��ͼΪһ�����õ糡���ų��Ե���˶����Ƶ�ģ��ͼ��������I�е�P1��P2�ֱ�Ϊ���ٵ糡�����������壬P2������һ�ף���������ֱƽ�����Է��ã���ʼ���д�СΪU�ĵ�ѹ�������������һ��l��l��Ϊ�߽����ֱ���µ���ǿ�糡�������������һ��l��Ϊ��߽紹ֱ��ֽ�����ǿ�ų�������һ����������ӣ��������ƣ�����Ϊm������Ϊq���Ӽ���P1�ɾ�ֹ��ʼ��������OO�䷽���������ӱ߽�l���P���뿪�����ʱ�ٶ���ˮƽ����нǦ�=30�㣮����P1��P2���������ӵ�ѹ��ΪU�䣬�����������䣬������ӱ߽�l���Q���뿪�����ʱ�ٶ���ˮƽ����нǦ�=60�㣮��֪PQ����ľ���Ϊd��
��ͼΪһ�����õ糡���ų��Ե���˶����Ƶ�ģ��ͼ��������I�е�P1��P2�ֱ�Ϊ���ٵ糡�����������壬P2������һ�ף���������ֱƽ�����Է��ã���ʼ���д�СΪU�ĵ�ѹ�������������һ��l��l��Ϊ�߽����ֱ���µ���ǿ�糡�������������һ��l��Ϊ��߽紹ֱ��ֽ�����ǿ�ų�������һ����������ӣ��������ƣ�����Ϊm������Ϊq���Ӽ���P1�ɾ�ֹ��ʼ��������OO�䷽���������ӱ߽�l���P���뿪�����ʱ�ٶ���ˮƽ����нǦ�=30�㣮����P1��P2���������ӵ�ѹ��ΪU�䣬�����������䣬������ӱ߽�l���Q���뿪�����ʱ�ٶ���ˮƽ����нǦ�=60�㣮��֪PQ����ľ���Ϊd����1����U���������е糡ǿ��E�Ĵ�С��
��2�������ν������������Ӿ��ܻص��߽�l����ͬһ�㣬��������дų��ĴŸ�Ӧǿ��B�Ĵ�С�ͷ����ų���Χ�㹻��
���� ��1�������������б����٣��������������ƽ���˶��������˶��ķֽⷨ������ţ�ٵڶ����ɡ��˶�ѧ��ʽ�Ͷ��ܶ����õ����ٵ�ѹU�������������ƫ��ǵĹ�ϵʽ�����ñ��������U�䣮PQ����ľ�����ڵ����������к�ƫ����������ţ�ٵڶ����ɺ��˶�ѧ��ʽ������E��
��2��������������ֻ����������������Բ���˶�������ţ�ٵڶ����ɺͼ��ι�ϵ���B���������ι켣�ҵij��ȴ�С�����������ת�ķ����ж�B�ķ���
���  �⣺��1�����ɾ�U����֮����ٶ�Ϊv0�����߽���ٶ�Ϊv����ֱ�����ƫ����Ϊy����ֱ���ٶ�Ϊvy���ٶ�ƫ���Ϊ�ȣ������Ŀ���ΪL������������ʱ��Ϊt�����ٶ�Ϊa��
�⣺��1�����ɾ�U����֮����ٶ�Ϊv0�����߽���ٶ�Ϊv����ֱ�����ƫ����Ϊy����ֱ���ٶ�Ϊvy���ٶ�ƫ���Ϊ�ȣ������Ŀ���ΪL������������ʱ��Ϊt�����ٶ�Ϊa��
����II����
L=v0t ��
y=$\frac{1}{2}$vyt ��
tan��=$\frac{{v}_{y}}{{v}_{0}}$ ��
���y=$\frac{L}{2}$tan�� ��
�糡�������ɶ��ܶ�����qU=$\frac{1}{2}$m${v}_{0}^{2}$ ��
��ţ�ٵڶ����ɣ�Eq=ma��
��y=$\frac{1}{2}$at2=$\frac{1}{2}\frac{qE}{m}{t}^{2}$=$\frac{1}{2}\frac{qE{L}^{2}}{m{v}_{0}^{2}}$=$\frac{qE{L}^{2}}{4qU}$ ��
�ɢܢ�ã�U=$\frac{EL}{2tan��}$ ��
���Դ�����ֵ�ã�$\frac{U��}{U}$=$\frac{tan��}{tan��}$=$\frac{1}{3}$
��ã�U��=$\frac{1}{3}$U
�ڶ���ƫ����y2���һ��ƫ����y1֮��Ϊ�ã�y2-y1=d
��Ϣܵã�
$\frac{L}{2}$tan��-$\frac{L}{2}$tan��=d
���L=$\sqrt{3}$d
�ɢߵã���һ������ʱU=$\frac{EL}{2tan��}$����ã�E=$\frac{2U}{3d}$
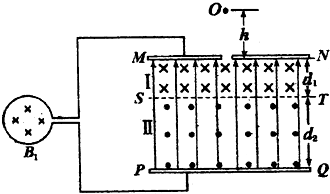
��2�������ų�ʱ��������Բ���˶��İ뾶ΪR
��ţ�ٵڶ����ɣ�qvB=m$\frac{{v}^{2}}{R}$
����v0=vcos��
��ã�R=$\frac{\sqrt{2q{U}_{m}}}{qBcos��}$
������ֵ�õ�����һ�����ӵİ뾶R1�͵ڶ������ӵİ뾶R2��ϵΪ��R1=R2
�������ҳ�֮��Ϊd
�ɵã�2R1cos��-2R2cos��=d
��ã�B=$\frac{6-2\sqrt{3}}{3d}\sqrt{\frac{2mU}{q}}$
�ɵ�һ���ҳ����ڵڶ����ҳ���֪Բ��λ��������·��������ֶ����жϵ�֪��B�ķ���ֱֽ�����⣮
�𣺣�1��U���СΪ$\frac{1}{3}$U������II�е糡ǿ��E=$\frac{2U}{3d}$��
��2������III�дų��ĴŸ�Ӧǿ��B=$\frac{6-2\sqrt{3}}{3d}\sqrt{\frac{2mU}{q}}$������ֱֽ�����⣮
���� �����ǵ糡���١�ƫת�ʹų���Բ���˶����ۺϣ��糡���ٸ��ݶ��ܶ������ɵ��ٶȣ��糡��ƫת�����˶��ĺϳ���ֽⷨ�о����ų��и���ţ�ٵڶ������о��켣�뾶���dz�����˼·��

| A�� | ָ������Խ�����һ���ż� | |
| B�� | ָ�����ܹ�ָ���ϱ���˵��������дų� | |
| C�� | ָ�����ָ���ܵ���������ĸ��� | |
| D�� | ��ָ�������Ϸ�������ָ�뷽�����һֱ���ߣ�����ͨ��ʱָ���벻ƫת |

| A�� | ��Դ���ܹ���һ����С | B�� | ��Դ���˵�ѹһ����С | ||
| C�� | R1�Ĺ���һ������ | D�� | R2�Ĺ���һ����С |
| A�� | ��������Ϊ$\frac{32{��}^{2}{R}^{3}}{G{T}^{2}}$ | B�� | ��������������ٶ�Ϊ$\frac{8{��}^{2}}{{T}^{2}}$R | ||
| C�� | �����ܶ�Ϊ$\frac{3��}{G{T}^{2}}$ | D�� | �����һ�����ٶ�Ϊ$\frac{4��R}{T}$ |
 ��ͼ��ʾ����֪һ����С���ڹ⻬��Ե��ˮƽ���ϴӾ�ֹ��ʼ����ѹU���ٺ�ˮƽ���뻥�ഹֱ����ǿ�糡E����ǿ�糡����ֱ������ǿ�ų�����ǿ�ų���ˮƽ���ĸ��ϳ��У�E��B��U��gΪ��֪����С���ڴ˿ռ����ֱ����������Բ���˶���������
��ͼ��ʾ����֪һ����С���ڹ⻬��Ե��ˮƽ���ϴӾ�ֹ��ʼ����ѹU���ٺ�ˮƽ���뻥�ഹֱ����ǿ�糡E����ǿ�糡����ֱ������ǿ�ų�����ǿ�ų���ˮƽ���ĸ��ϳ��У�E��B��U��gΪ��֪����С���ڴ˿ռ����ֱ����������Բ���˶���������| A�� | С����ܴ����� | |
| B�� | С��������Բ���˶��İ뾶Ϊr=$\frac{1}{B}$$\sqrt{\frac{2UE}{g}}$ | |
| C�� | ����ѹU������С��������Բ���˶������ڱ�� | |
| D�� | ��ǿ�糡����һ����ֱ���� |
| A�� | ��������������Ļ�е������m��g-a��h | |
| B�� | �����������������������mah | |
| C�� | ���������������������������m��a+g��h | |
| D�� | ��������������˷���������mgh |
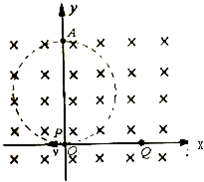 ��ͼ��ʾ����XOY����ϵ���д�ֱ��XOY����ƽ��ķ�Χ�㹻�����ǿ�ų����Ÿ�Ӧǿ��ΪB��ijʱ������������P��Q�ֱ������ԭ��O��X���ϵ�Q��ͬʱ��ʼ�˶��������Ӵ�ͬ�ֵ�ɣ���������Ϊq��������Ϊm��P���ӵij��ٶȷ�����X�Ḻ�����ٶȴ�СΪV���˶��켣��ͼ��������ʾ��Q���ӳ��ٶȷ�������XOYƽ�������п��ܵķ���Q�㵽O��ľ�����P���ӹ���뾶��1.5���������������������ƣ�
��ͼ��ʾ����XOY����ϵ���д�ֱ��XOY����ƽ��ķ�Χ�㹻�����ǿ�ų����Ÿ�Ӧǿ��ΪB��ijʱ������������P��Q�ֱ������ԭ��O��X���ϵ�Q��ͬʱ��ʼ�˶��������Ӵ�ͬ�ֵ�ɣ���������Ϊq��������Ϊm��P���ӵij��ٶȷ�����X�Ḻ�����ٶȴ�СΪV���˶��켣��ͼ��������ʾ��Q���ӳ��ٶȷ�������XOYƽ�������п��ܵķ���Q�㵽O��ľ�����P���ӹ���뾶��1.5���������������������ƣ�