题目内容
【题目】一列汽车车队以v1=10 m/s的速度匀速行驶,相邻车间距为25 m,后面有一辆摩托车以v2=20 m/s的速度同向行驶,当它与车队最后一辆车相距S0=40 m时刹车,以a=0.5 m/s2的加速度做匀减速直线运动,摩托车从车队旁边行驶而过,设车队车辆数n足够多,问:
(1)摩托车最多能与几辆汽车相遇?
(2)摩托车从赶上车队到离开车队,共经历多少时间?(结果可用根号表示)
【答案】(1)3辆 (2)8![]() s
s
【解析】(1)当摩托车速度减为10 m/s时,设用时为t,摩托车行驶的距离为x1,每辆汽车行驶的距离都为x2.
由速度公式得:v2=v1-at
解得t=20 s
由速度位移公式得:v22-v12v=-2ax1
解得x1=300 m
x2=v2t=200 m
摩托车与最后一辆汽车的距离:Δx=(300-200-40) m=60 m
故摩托车追上的汽车数n=![]() +1=3.4,则追上汽车3辆.
+1=3.4,则追上汽车3辆.
(2)设摩托车追上最后一辆汽车的时刻为t1,最后一辆汽车超过摩托车的时刻为t2.
则:Δx+v2t=v1t-![]() at2
at2
解得:Δt=t2-t1=8![]() s.
s.

【题目】在“探究弹力和弹簧伸长的关系”时,某同学把两根弹簧如图连接起来进行探究。在弹性限度内将50g的钩码逐个挂在弹簧下端,依次得到指针A、B的示数![]() 和
和![]() 如表所示。
如表所示。
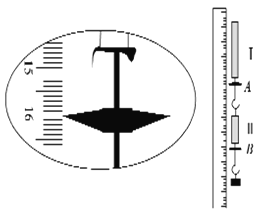
钩码数 | 1 | 2 | 3 | 4 |
| 15.71 | 19.71 | 23.70 | 27.72 |
| 29.96 | 35.76 | 41.51 | 47.36 |
(1)由表中数据可知,该刻度尺的最小刻度值为________mm。某次测量如图所示,指针示数为________cm。
(2)用表中数据计算弹簧Ⅰ的劲度系数为________N/m(结果保留三位有效数字,重力加速度g取![]() )。由表中数据_________(填“能”或“不能”)计算出弹簧Ⅱ的劲度系数。
)。由表中数据_________(填“能”或“不能”)计算出弹簧Ⅱ的劲度系数。