题目内容
20.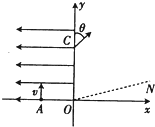 如图所示,在平面直角坐标系xOy中的第一象限内存在磁感应强度大小为B、方向垂直于坐标平面向内的有界圆形匀强磁场区域(图中未画出);在第二象限内存在沿x轴负方向的匀强电场.一粒子源固定在x轴上的A点,A点坐标为(-L,0).粒子源沿y轴正方向释放出速度大小为v的电子,电子恰好能通过y轴上的C点,C点坐标为(0,2L),电子经过磁场偏转后恰好垂直通过第一象限内与x轴正方向成15°角的射线ON(已知电子的质量为m,电荷量为e,不考虑粒子的重力和粒子之间的相互作用).求:
如图所示,在平面直角坐标系xOy中的第一象限内存在磁感应强度大小为B、方向垂直于坐标平面向内的有界圆形匀强磁场区域(图中未画出);在第二象限内存在沿x轴负方向的匀强电场.一粒子源固定在x轴上的A点,A点坐标为(-L,0).粒子源沿y轴正方向释放出速度大小为v的电子,电子恰好能通过y轴上的C点,C点坐标为(0,2L),电子经过磁场偏转后恰好垂直通过第一象限内与x轴正方向成15°角的射线ON(已知电子的质量为m,电荷量为e,不考虑粒子的重力和粒子之间的相互作用).求:(1)第二象限内电场强度E的大小.
(2)电子离开电场时的速度方向与y轴正方向的夹角θ
(3)圆形磁场的最小半径Rm.
分析 (1)粒子在电场中做类似平抛运动,x方向匀速,y方向匀加速,根据运动学公式列式求解;
(2)先根据运动学公式列式求解出x、y方向的分速度,然后根据几何关系列式求解;也可以根据类似平抛运动速度偏转角的正切是位移偏转角正切的2倍直接求解;
(3)先根据洛伦兹力提供向心力求解出轨迹的半径,然后画出轨迹图,确定磁场的最小半径
解答  解:(1)从A到C的过程中,电子做类平抛运动,有:
解:(1)从A到C的过程中,电子做类平抛运动,有:
x方向:$L=\frac{1}{2}a{t}^{2}=\frac{eE}{2m}{t}^{2}$
x方向:2L=vt
联立解得:$E=\frac{m{v}^{2}}{2eL}$
(2)设电子到达C点的速度大小为vc,方向与y轴正方向的夹角为θ.
由动能定理,有:$\frac{1}{2}{mv}_{C}^{2}-\frac{1}{2}m{v}^{2}=eEL$
解得:${v}_{C}=\sqrt{2}v$
故有:$cosθ=\frac{v}{{v}_{C}}=\frac{\sqrt{2}}{2}$
得:θ=45°
(3)画轨迹如图所示,电子在磁场中做匀速圆周运动的半径为:
$r=\frac{m{v}_{C}}{r}$
电子在磁场中偏转120°后垂直于ON射出.磁场最小半径为:
${R}_{m}=\frac{PQ}{2}=rsin60°$
得:${R}_{m}=\frac{\sqrt{6}mv}{2eB}$
答:(1)匀强电场的电场强度E的大小为$\frac{m{v}^{2}}{2eL}$;
(2)电子离开电场时的速度方向与y轴正方向的夹角θ为45°;
(3)圆形磁场的最小半径Rm为$\frac{\sqrt{6}mv}{2eB}$
点评 本题中粒子先在电场中做类似平抛运动,然后进入磁场做匀速圆周运动,要注意两个轨迹的连接点,然后根据运动学公式和牛顿第二定律以及几何关系列式求解,其中画出轨迹是关键

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 图示的电路中电表均为理想电表,电源为恒流电源,即不管外电路情况如何变化,它都能提供持续且恒定的电流.则当滑动变阻器R0的滑动端向上滑动时,电压表示数的变化量与电流表示数变化量之比的绝对值等于( )
图示的电路中电表均为理想电表,电源为恒流电源,即不管外电路情况如何变化,它都能提供持续且恒定的电流.则当滑动变阻器R0的滑动端向上滑动时,电压表示数的变化量与电流表示数变化量之比的绝对值等于( )| A. | R0 | B. | R1 | C. | R2 | D. | 电源内阻r |
 如图所示,导热的气缸固定在水平地面上,用活塞把一定质量的理想气体封闭在气缸内,气缸的内壁光滑.现用水平外力F作用于活塞杆,使活塞缓慢地向右移动,并由状态I变化到状态Ⅱ,在此过程中如果环境保持恒温,下列说法中正确的是( )
如图所示,导热的气缸固定在水平地面上,用活塞把一定质量的理想气体封闭在气缸内,气缸的内壁光滑.现用水平外力F作用于活塞杆,使活塞缓慢地向右移动,并由状态I变化到状态Ⅱ,在此过程中如果环境保持恒温,下列说法中正确的是( )| A. | 每个气体分子的速率都保持不变 | B. | 气体分子的平均动能不变 | ||
| C. | 气体内能减小 | D. | 气体放热 |
 如图所示,甲、乙两个质量相同、带等量异种电荷的带电粒子,以不同的速率经小孔P从磁场边界MN,进入方向垂直纸面向里的匀强磁场中,在磁场中作匀速圆周运动,并垂直磁场边界MN射出磁场,半圆轨迹如图中虚线所示,不计粒子所受的重力及空气阻力,则下列说法中正确的是( )
如图所示,甲、乙两个质量相同、带等量异种电荷的带电粒子,以不同的速率经小孔P从磁场边界MN,进入方向垂直纸面向里的匀强磁场中,在磁场中作匀速圆周运动,并垂直磁场边界MN射出磁场,半圆轨迹如图中虚线所示,不计粒子所受的重力及空气阻力,则下列说法中正确的是( )| A. | 甲带负电荷,乙带正电荷 | |
| B. | 洛伦兹力对甲做功 | |
| C. | 甲的速率大于乙的速率 | |
| D. | 甲在磁场中运动的时间大于乙在磁场中运动的时间 |
| A. | 至少增大到原来的4倍 | B. | 至少增大到原来的2倍 | ||
| C. | 至少增大到原来的3倍 | D. | 减少到原来的一半 |

 如图所示放在水平面上的小车上表面水平,AB是半径为R的$\frac{1}{4}$光滑圆弧轨道,下端B的切线水平且与平板车上表面平齐,车的质量为M.现有一质量为m的小滑块,从轨道上端A处无初速释放,滑到B端后,再滑到平板车上.若车固定不动,小滑块恰不能从车上掉下.(重力加速度为g):
如图所示放在水平面上的小车上表面水平,AB是半径为R的$\frac{1}{4}$光滑圆弧轨道,下端B的切线水平且与平板车上表面平齐,车的质量为M.现有一质量为m的小滑块,从轨道上端A处无初速释放,滑到B端后,再滑到平板车上.若车固定不动,小滑块恰不能从车上掉下.(重力加速度为g):