题目内容
12. 如图所示放在水平面上的小车上表面水平,AB是半径为R的$\frac{1}{4}$光滑圆弧轨道,下端B的切线水平且与平板车上表面平齐,车的质量为M.现有一质量为m的小滑块,从轨道上端A处无初速释放,滑到B端后,再滑到平板车上.若车固定不动,小滑块恰不能从车上掉下.(重力加速度为g):
如图所示放在水平面上的小车上表面水平,AB是半径为R的$\frac{1}{4}$光滑圆弧轨道,下端B的切线水平且与平板车上表面平齐,车的质量为M.现有一质量为m的小滑块,从轨道上端A处无初速释放,滑到B端后,再滑到平板车上.若车固定不动,小滑块恰不能从车上掉下.(重力加速度为g):(1)求滑块到达B端之前瞬间所受支持力的大小;
(2)求滑块在车上滑动的过程中,克服摩擦力做的功;
(3)若车不固定,且地面光滑,把滑块从A点正上方的P点无初速释放,P点到A点的高度为h,滑块从A点进入轨道,最后恰停在车的中点.求车的长度.(滑块与小车的摩擦因数为μ)
分析 (1)根据动能定理求出到达B点的速度,结合牛顿第二定律求出支持力的大小,从而得出压力的大小.
(2)对滑上小车的过程,根据动能定理求出克服摩擦力做功的大小.
(3)根据动能定理求出滑块到达最低点的速度,结合动量守恒求出滑块和小车的共同速度,根据能量守恒定律求出车的长度.
解答 解:(1)根据动能定理得:
$mgR=\frac{1}{2}m{{v}_{B}}^{2}$,
解得:${v}_{B}=\sqrt{2gR}$,
根据牛顿第二定律得:$N-mg=m\frac{{{v}_{B}}^{2}}{R}$,
解得:N=3mg.
(2)根据动能定理得:$-{W}_{f}=0-\frac{1}{2}m{{v}_{B}}^{2}$,
解得:${W}_{f}=\frac{1}{2}m{{v}_{B}}^{2}=mgR$.
(3)根据动能定理得:$mg(h+R)=\frac{1}{2}m{v}^{2}$,
解得:v=$\sqrt{2g(h+R)}$,
物块与小车组成的系统动量守恒,规定物块的速度方向为正方向,根据动量守恒定律得:mv=(M+m)v′,
解得:$v′=\frac{mv}{M+m}$,
根据能量守恒得:$μmg\frac{L}{2}=\frac{1}{2}m{v}^{2}-\frac{1}{2}(M+m)v{′}^{2}$,
解得:L=$\frac{2M(h+R)}{μ(M+m)}$.
答:(1)滑块到达B端之前瞬间所受支持力的大小为3mg;
(2)克服摩擦力做的功为mgR;
(3)车的长度为$\frac{2M(h+R)}{μ(M+m)}$.
点评 本题考查了动能定理、动量守恒定律、能量守恒定律的综合运用,综合性较强,对学生的能力要求较高,对于第三问,也可以根据动力学知识求解,但是没有运用动量和能量综合求解简捷.

 在“测电源电动势和内阻”的实验中,某同学作出了两个电源路端电压U与电流I的关系图线,如图所示.两个电源的电动势分别为E1、E2,内阻分别为r1、r2.如果外电路分别接入相同的电阻R,则两个电源的( )
在“测电源电动势和内阻”的实验中,某同学作出了两个电源路端电压U与电流I的关系图线,如图所示.两个电源的电动势分别为E1、E2,内阻分别为r1、r2.如果外电路分别接入相同的电阻R,则两个电源的( )| A. | 路端电压和电流不可能同时相等 | B. | 输出功率不可能相等 | ||
| C. | 总功率不可能相等 | D. | 效率不可能相等 |

| A. | 若原子核D和E结合成原子核F,结合过程一定会释放能量 | |
| B. | 若原子核D和E结合成原子核F,结合过程一定要吸收能量 | |
| C. | 若原子核A分裂成原子核B和C,分裂过程一定要释放能量 | |
| D. | 若原子核A分裂成原子核B和C,分裂过程一定要吸收能量 |
 如图所示,在直线坐标系中x=d处放置点电荷-Q,x=-d处放置点电荷Q(Q>0),P点位于x=$\frac{1}{2}$d处.下列半段正确的是( )
如图所示,在直线坐标系中x=d处放置点电荷-Q,x=-d处放置点电荷Q(Q>0),P点位于x=$\frac{1}{2}$d处.下列半段正确的是( )| A. | 在x轴上有2个点与P点电势强度相同 | |
| B. | 选无穷远处电势为零,则坐标原点O的电势为正 | |
| C. | 电子(不计重力)从P点移动到坐标原点O的过程中电势能将减小 | |
| D. | 电子(不计重力)从P点移动到坐标原点O的过程中加速度将增大 |
| A. | 0.6v | B. | 0.2v | C. | 0.3v | D. | 0.22v |
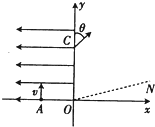 如图所示,在平面直角坐标系xOy中的第一象限内存在磁感应强度大小为B、方向垂直于坐标平面向内的有界圆形匀强磁场区域(图中未画出);在第二象限内存在沿x轴负方向的匀强电场.一粒子源固定在x轴上的A点,A点坐标为(-L,0).粒子源沿y轴正方向释放出速度大小为v的电子,电子恰好能通过y轴上的C点,C点坐标为(0,2L),电子经过磁场偏转后恰好垂直通过第一象限内与x轴正方向成15°角的射线ON(已知电子的质量为m,电荷量为e,不考虑粒子的重力和粒子之间的相互作用).求:
如图所示,在平面直角坐标系xOy中的第一象限内存在磁感应强度大小为B、方向垂直于坐标平面向内的有界圆形匀强磁场区域(图中未画出);在第二象限内存在沿x轴负方向的匀强电场.一粒子源固定在x轴上的A点,A点坐标为(-L,0).粒子源沿y轴正方向释放出速度大小为v的电子,电子恰好能通过y轴上的C点,C点坐标为(0,2L),电子经过磁场偏转后恰好垂直通过第一象限内与x轴正方向成15°角的射线ON(已知电子的质量为m,电荷量为e,不考虑粒子的重力和粒子之间的相互作用).求: 如图所示,水平面光滑,一辆长度为l的平板小车A上表面粗糙,可看做质点的小物块B在小车右端、小车质量是小物块质量的2倍,小车和小物块一起以相同的速度v0与墙壁发生弹性碰撞,小车速度瞬间反向,当小物块与小车相对静止时,小物块在距离小车右端$\frac{2l}{3}$处,重力加速度为g,求小物块在小车上滑行的时间.
如图所示,水平面光滑,一辆长度为l的平板小车A上表面粗糙,可看做质点的小物块B在小车右端、小车质量是小物块质量的2倍,小车和小物块一起以相同的速度v0与墙壁发生弹性碰撞,小车速度瞬间反向,当小物块与小车相对静止时,小物块在距离小车右端$\frac{2l}{3}$处,重力加速度为g,求小物块在小车上滑行的时间. 如图所示,一个理想变压器的原线圈接在220V的市电上,向额定电压为1.10×104V的霓虹灯供电,使它正常发光.为了安全,需在原线圈回路中接入熔断器,使副线圈电路中电流超过12mA时,熔丝就熔断.求熔丝的熔断电流.
如图所示,一个理想变压器的原线圈接在220V的市电上,向额定电压为1.10×104V的霓虹灯供电,使它正常发光.为了安全,需在原线圈回路中接入熔断器,使副线圈电路中电流超过12mA时,熔丝就熔断.求熔丝的熔断电流. 如图,可视为质点的小球A、B用不可伸长的细软轻线连接,跨过固定在地面上半径为R有光滑圆柱,A的质量为B的两倍.当B位于地面时,A恰与圆柱轴心等高.将A由静止释放.
如图,可视为质点的小球A、B用不可伸长的细软轻线连接,跨过固定在地面上半径为R有光滑圆柱,A的质量为B的两倍.当B位于地面时,A恰与圆柱轴心等高.将A由静止释放.