题目内容
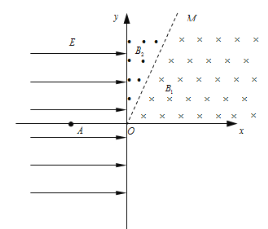
【题目】如图所示,在第一象限内有垂直纸面向里和向外的匀强磁场,磁感应强度分别为B1=0.1T、B2=0.05T,分界线OM与x轴正方向的夹角为α.在第二、三象限内存在着沿x轴正方向的匀强电场,电场强度E=1×104V/m.现有一带电粒子由x轴上A点静止释放,从O点进入匀强磁场区域.已知A点横坐标xA=5×10-2m,带电粒子的质量m=1.6×10-24kg,电荷量q=+1.6×10-15C.
(1)求粒子到达O点时的速度大小;
(2)如果α=30°,则粒子能经过OM分界面上的哪些点?
(3)如果α=30°,让粒子在OA之间的某点释放,要求粒子仍能经过(2)问中的那些点,则粒子释放的位置应满足什么条件?
【答案】(1) ![]() ;(2) l=(3k2)×102m(k=1、2、3…)或l=3k′×102m(k′=1、2、3…);(3)
;(2) l=(3k2)×102m(k=1、2、3…)或l=3k′×102m(k′=1、2、3…);(3) ![]() 或
或![]()
【解析】
(1)根据动能定理可知
![]()
解得粒子到达O点时的速度大小:
![]()
(2) 当α=30°时,粒子每次在任意一个磁场中运动的圆弧的圆心角均为60°,弦长均等于半径.粒子在磁场B1中运动
![]()
解得:
r1=1×102m,
同理粒子在磁场B2中运动的半径
r2=2r1=2×102m
OM上经过的点距离O点的距离是
l=kr1+(k1)r2=(3k2)r1=(3k2)×102m(k=1、2、3…)
或
l=k′(r1+r2)=3k′×102m(k′=1、2、3…)
(3) 要仍然经过原来的点,需满足
r1=n(r1′+r2′)(n=1、2、3…)
解得
![]()
即
![]()
根据匀变速规律可知,粒子释放的位置应满足
![]()
或者
r1=n′(2r1′′+r2′′)(n′=1、2、3…)
解得:
![]()
即
![]()
粒子释放的位置应满足
![]()

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目