题目内容
【题目】如图，固定在竖直平面内的倾斜轨道AB，与水平光滑轨道BC相连，竖直墙壁CD高
，紧靠墙壁在地面固定一个和CD等高，底边长
的斜面，一个质量
的小物块
视为质点
在轨道AB上从距离B点
处由静止释放，从C点水平抛出，已知小物块在AB段与轨道间的动摩擦因数为
，达到B点时无能量损失；AB段与水平面的夹角为
重力加速度
，
，
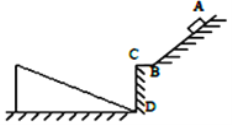
(1)求小物块运动到B点时的速度大小；
(2)求小物块从C点抛出到击中斜面的时间；
(3)改变小物块从轨道上释放的初位置，求小物块击中斜面时动能的最小值.
【答案】(1)
(2)
(3)
【解析】
(1)对滑块从A到B过程，根据动能定理列式求解末速度；
(2)从C点画出后做平抛运动，根据分位移公式并结合几何关系列式分析即可；
(3)动能最小时末速度最小，求解末速度表达式分析即可.
对滑块从A到B过程，根据动能定理，有：
，
解得：
；
设物体落在斜面上时水平位移为x，竖直位移为y，画出轨迹，如图所示：
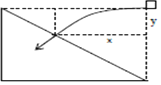
对平抛运动，根据分位移公式，有：
，
，
结合几何关系，有：
，
解得：
；
对滑块从A到B过程，根据动能定理，有：，
对平抛运动，根据分位移公式，有：
，
，
结合几何关系，有：，
从A到碰撞到斜面过程,根据动能定理有：
联立解得：
，
故当
，即
时，动能
最小为：
；
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
