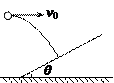题目内容

如图所示，从倾角为θ的足够长斜面上的A点，先后将同一小球以不同的初速度水平向右抛出．第一次初速度为V1；球落到斜面上瞬时速度方向与斜面夹角为α1；第二次初速度为V2；球落到斜面上瞬时速度方向与斜面夹角为α2，不计空气阻力，若V1＞V2，则α1______α2（填＞、=、＜）
平抛运动落在斜面上时，竖直方向的位移和水平方向上位移比值一定：tanθ=
y
x
=
1
2
gt2
v0t

解得：t=
2v0tanθ
g
．
则落在斜面上时竖直方向上的分速度vy=gt=2v0tanθ．
设速度与水平方向的夹角为α，有tanα=
vy
v0
=2tanθ．知落在斜面上时，速度与水平方向的夹角与初速度无关，则小球与水平方向的夹角相同，因为速度方向与斜面的夹角等于速度与水平方向的夹角减去斜面的倾角，所以α1=α2．
故答案为：=
练习册系列答案
相关题目
如图甲，喷出的水做斜抛运动，图乙为斜抛运动的轨迹，对轨迹上的两点A、B下列说法中正确的是（不计空气阻力）（　　）
A．A点的速度方向沿切线向下，合力方向竖直向上
B．A点的速度方向沿切线向上，合力方向竖直向下
C．B点的速度方向沿切线向上，合力方向竖直向下
D．B点的速度方向沿切线向下，合力方向竖直向上
如图，以10m/s的水平初速度抛出的物体，飞行一段时间后，垂直撞在倾角为30?的斜面上，若g取10m/s2，可知物体飞行的时间为（　　）
A．2sB．
3
3
s		C．
2
3
3
s		D．
3
s
一个物体被水平抛出，抛出后第1秒、第2秒、第3秒内竖直下落的距离之比为______，通过的水平距离之比为______．
物体作平抛运动，在如图所示的四幅图中，能正确描述物体在竖直方向的分速度Vy（取向下为正）随时间t变化的图线的是（　　）
A．B．C．D．
从竖直墙的前方A处，沿AO方向水平发射三颗弹丸a、b、c，在墙上留下的弹痕如图所示．已知Oa=ab=bc，则a、b、c三颗弹丸（　　）
A．初速度之比是
6
：
3
：
2
B．初速度之比是1：
2
：
3
C．从射出至打到墙上过程速度增量之比是1：
2
：
3
D．从射出至打到墙上过程速度增量之比是
6
：
3
：
2
在距离地面5米处将一个质量为1kg的小球以10m/s的速度水平抛出（g取10m/s2），问
（1）小球在空中的飞行时间是多少？
（2）水平飞行的距离是多少米？
（3）求小球落地时的速度大小．
如图所示，一架在H=2000m高空以v0=200m/s的速度水平匀速飞行的轰炸机，要想用两枚炸弹分别炸山脚和山顶的目标A和B，已知相对飞机自由释放炸弹，山高h=720m，山脚与山顶的水平距离为s=1200m，若不计空气阻力，g取10m/s2，求：
（1）第一枚炸弹在到达目标A时，其速度方向与水平地面的夹角θ是多少度？
（2）两次释放的炸弹在空中飞行的水平距离分别是多少？
（3）两次释放炸弹的时间间隔△t是多少？
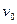如图所示，以水平初速度抛出的物体，飞行一段时间后，垂直撞在倾角为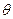的斜面上，求物体完成这段飞行的时间和位移。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网