题目内容
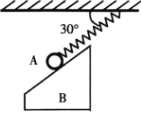
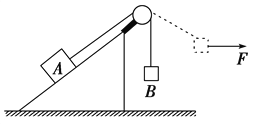
【题目】如图1所示,用一水平外力F拉着一个静止在倾角为θ的光滑斜面上的物体,逐渐增大F,物体做变加速运动,其加速度a随外力F变化的图象如图2示,若重力加速度g取10m/s2 , 根据图中所提供的信息求解
(1)斜面的倾角的正弦值为多少?物体的质量为多少?
(2)物体能静止在斜面上所施加的最小外力为多大?
【答案】
(1)解:由图知,当F=0时,物体向下的加速度a=6m/s2,根据牛顿第二定律得:
mgsinθ=mas
得:sinθ=0.6.
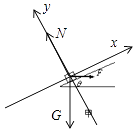
对物体受力分析,受推力、重力、支持力,如图,根据牛顿第二定律,
当F=20N时,物体向上的加速度为:a=2m/s2
Fcosθ﹣mgsinθ=ma
可得:m=2kg
答:斜面的倾角的正弦值为0.6,物体的质量为2kg.
(2)解:由三力平衡得物体能静止在斜面上有:Fcosθ﹣mgsinθ=0
所施加的沿水平方向的最小外力为:F=15 N
答:物体能静止在斜面上所施加的最小外力为15N.
【解析】(1)由图知道,F=0时,物体向下的加速度为 a=6m/s2,对物体受力分析,根据牛顿第二定律列式.当F=20N时,物体向上的加速度为a=2m/s2,根据牛顿第二定律列式,联立可求解.(2)物体能静止在斜面上时,由三力平衡求所施加的最小外力.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目