��Ŀ����
����Ŀ����ƽ������ϵ�ڣ��ڵ�1����������y�Ḻ�������ǿ�糡���ڵ�III��IV�������д�ֱ����ƽ���������ǿ�ų�����y����y=l������x������һ�Ⱥ�Ϊ ![]() ���ٶ�Ϊv0�Ĵ��������ӣ���x=2l��M���뿪�糡�����ų����ٴε���x��ʱ�պô�����ԭ��O������������������������
���ٶ�Ϊv0�Ĵ��������ӣ���x=2l��M���뿪�糡�����ų����ٴε���x��ʱ�պô�����ԭ��O������������������������
��1����ǿ�糡�ij�ǿE����ǿ�ų��ĴŸ�Ӧǿ��B�Ĵ�С��
��2�����Ӵ�A�˶���O������ʱ�䣻
��3�����ø����Ӵ�y��y��0������λ��P������x�����䣨�����ٶ�v0���䣩�������ڶ���ͨx��ʱ�ĺ����꣮
���𰸡�
��1���⣺�����ڵ糡��ֻ�ܵ糡�����ã���ƽ���˶������ԣ��У�
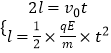 ��
��
������ ![]() =
= ![]() ��
��
����ƽ���˶��Ĺ��ɿ�֪�������ڵ糡���˶���ʱ��Ϊ�� ![]() ������ų�ʱ���ٶ�v��ˮƽ����Ϊ��vx=v0����ֱ����Ϊ��
������ų�ʱ���ٶ�v��ˮƽ����Ϊ��vx=v0����ֱ����Ϊ�� ![]() ��
��
��ã� ![]() ��
��
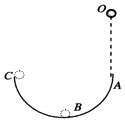
�����ڴų���ֻ��������������������������������Բ���˶������ԣ������˶��켣��ͼ��ʾ��
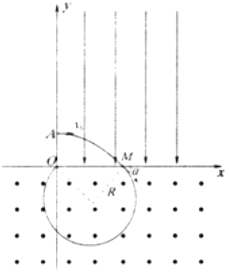
��������Բ���˶��İ뾶Ϊ�� ![]() ��
��
���ԣ��������������������ɵã� ![]() ��
��
��ã� ![]() ��
��
����ǿ�糡�ij�ǿE�Ĵ�СΪ ![]() ����ǿ�ų��ĴŸ�Ӧǿ��B�Ĵ�СΪ
����ǿ�ų��ĴŸ�Ӧǿ��B�Ĵ�СΪ ![]() ��
��
��2���ɣ�1����֪�������ڵ糡�е��˶�ʱ��Ϊ ![]() ��
��
�����ڴų���ת�������Ľ�Ϊ270�㣬Բ���˶�������Ϊ�� ![]() ��
��
���ԣ������ڴų��е��˶�ʱ��Ϊ�� ![]() ��
��
���ԣ����Ӵ�A�˶���O������ʱ��Ϊ ![]() ��
��
�����Ӵ�A�˶���O������ʱ��Ϊ ![]() ��
��
��3�������ڵ糡��ֻ�ܵ糡�����ã���ƽ���˶������ԣ��� 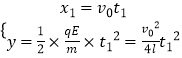 �����ԣ�
�����ԣ� ![]() ��
��
���ԣ������� ![]() �����ٶ�v�����ų���v���ˮƽ����Ϊv0����ֱ����Ϊ
�����ٶ�v�����ų���v���ˮƽ����Ϊv0����ֱ����Ϊ ![]() ��
��
���ԣ� ![]() �����ԣ������˶��켣��ͼ��
�����ԣ������˶��켣��ͼ��
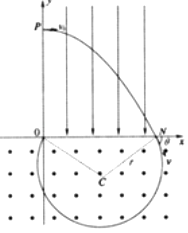
������ 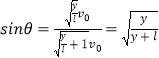
���������������������������ԣ� ![]() ��
��
��Բ���˶��ĶԳ��Կ�֪�������ڴų����˶���x���Ͻصõ��ҳ�Ϊ ![]() ��
��
��Ϊ�ҳ��������������꣬���ԣ�����һ����O���뿪�ų������ԣ����ӵڶ���ͨ��x��ʱ�ĺ�����Ϊx=0��
�����ø����Ӵ�y��y��0������λ��P������x�����䣨�����ٶ�v0���䣩�������ڶ���ͨ��x��ʱ�ĺ�����Ϊ0��
����������1�������ڵ糡������ƽ���˶������˶��ֽˮƽ����ֱ������ʽ��⡣
��2����ƽ���˶�����ֱλ�����˶�ʱ�䣬���ɼ��ι�ϵ���Բ���˶������Ľǣ����������˶���������˶�ʱ�䣬�ڵ糡���ų��е��˶�ʱ����Ӽ��ɵ����ӵ��˶�ʱ�䣻
��3��������ƽ���˶����ɣ��ٽ��Բ���˶��ĶԳ��ԣ�ͨ���뾶�����x���ϵ��ҳ���������������뿪�ų���λ�ã����ڶ���ͨ��x���λ�ã�

 �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�